L'espace
![]() invoqué par le postulat I doit être un espace de Hilbert
complet et séparable. Ces qualificatifs signifient que cet espace est doté
des propriétés mathématiques qui peuvent être résumées simplement
ci-après, d'une manière plus adaptée à leur utilisation future.
invoqué par le postulat I doit être un espace de Hilbert
complet et séparable. Ces qualificatifs signifient que cet espace est doté
des propriétés mathématiques qui peuvent être résumées simplement
ci-après, d'une manière plus adaptée à leur utilisation future.
![]() est un espace vectoriel défini sur le corps
est un espace vectoriel défini sur le corps
![]() des nombres complexes. Tout élément de
des nombres complexes. Tout élément de ![]() est
appelé vecteur ket ou simplement
est
appelé vecteur ket ou simplement ![]() et noté
et noté ![]() ou
ou
![]() ou
ou ![]() ou
ou ![]() ...
...
Le nombre de dimensions de ![]() peut être infini et il
existe alors des ensembles dénombrables de kets
peut être infini et il
existe alors des ensembles dénombrables de kets
![]() , appelés
, appelés ![]() , tels que :
, tels que :
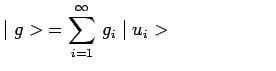 |
Cette propriété mathématique de décomposition d'un vecteur sur une base jouera dans le formalisme quantique un rôle capital car c'est elle qui permet d'exprimer mathématiquement le principe de superposition des états.
L'ensemble ![]() des formes linéaires notées
des formes linéaires notées ![]() ,
, ![]() ,
,
![]() etc appliquées aux éléments de
etc appliquées aux éléments de ![]() et à valeurs dans
et à valeurs dans
![]() tel que :
tel que :
peut être doté des lois de composition interne :
qui font de ![]() un autre espace vectoriel qui a
le même nombre de dimensions que
un autre espace vectoriel qui a
le même nombre de dimensions que ![]() . Le nouvel espace
vectoriel
. Le nouvel espace
vectoriel ![]() s'appelle l'espace dual de
s'appelle l'espace dual de ![]() et ses éléments notés
et ses éléments notés ![]() ,
,
![]() etc sont
appelés vecteurs bras ou ``
etc sont
appelés vecteurs bras ou ``![]() ''.
''.
Il existe une correspondance
![]() entre
entre ![]() et
et ![]() de
telle sorte qu'à tout bra
de
telle sorte qu'à tout bra ![]() de
de ![]() correspond un ket noté
correspond un ket noté
![]() de
de ![]() et vice-versa :
et vice-versa :
Cette correspondance est anti-linéaire ce qui signifie :
 |
Tout état physique peut donc être codé indifféremment par
des kets
![]() ou les bras images
ou les bras images
![]()
![]() est alors doté d'un produit scalaire qui, à
deux vecteurs ordonnés
est alors doté d'un produit scalaire qui, à
deux vecteurs ordonnés ![]() et
et ![]() de
de ![]() fait
correspondre un élément noté
fait
correspondre un élément noté ![]() de
de ![]() :
:
et dont la notation précise qu'il s'agit de la valeur prise par le bra
![]() sur le ket
sur le ket ![]() et donc d'une application bi-linéaire de
et donc d'une application bi-linéaire de
![]() dans
dans ![]() . En raison de la correspondance
anti-linéaire entre
. En raison de la correspondance
anti-linéaire entre ![]() et
et ![]() ce produit scalaire est
linéaire par rapport au ket
ce produit scalaire est
linéaire par rapport au ket ![]() et linéaire par rapport au bra
et linéaire par rapport au bra
![]() et donc antilinéaire par rapport au ket
et donc antilinéaire par rapport au ket ![]() .
.
Le produit scalaire est défini positif dans ![]() . De
ce qui précède il résulte que
. De
ce qui précède il résulte que
![]() et
et ![]() sont fonctions linéaires de
sont fonctions linéaires de ![]() et antilinéaires de
et antilinéaires de ![]() . Il peut donc être postulé que ces deux quantités sont
égales :
. Il peut donc être postulé que ces deux quantités sont
égales :
d'où quel que soit
![]()
Enfin l'espace ![]() est choisi tel que la norme
est choisi tel que la norme
![]() de tout vecteur
de tout vecteur ![]() est strictement
positive, c'est-à-dire telle que :
est strictement
positive, c'est-à-dire telle que :
![]() désignant l'élément neutre de l'espace
désignant l'élément neutre de l'espace
![]() .
.
Il a déjà été dit combien est capitale la propriété de
décomposition d'un vecteur ket sur une base dénombrable :
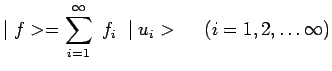 |
car c'est elle qui permet d'exprimer le principe de superposition. Néanmoins
cette propriété doit être elle-même généralisée pour que l'espace
![]() des états puisse constituer un cadre suffisant au formalisme
quantique.
des états puisse constituer un cadre suffisant au formalisme
quantique.
En effet, considérons par exemple la représentation
électromagnétique qu'il y a lieu de donner à un photon en
mouvement dans l'espace. Puisque ce photon décrit un paquet
d'énergie approximativement localisée, la physique
classiqueI12 représente cet état
par un potentiel vecteur
![]() ou les champs
électriques
ou les champs
électriques
![]() et magnétiques
et magnétiques
![]() qui ne prennent de valeurs sensibles que dans
cette région très réduite de l'espace physique où se trouve
approximativement localisé ce grain d'énergie, c'est-à-dire le photon.
qui ne prennent de valeurs sensibles que dans
cette région très réduite de l'espace physique où se trouve
approximativement localisé ce grain d'énergie, c'est-à-dire le photon.
Mathématiquement cela implique que ces fonctions vectorielles ou plutôt
chacune de leurs composantes, par exemple ![]() , soit de la forme :
, soit de la forme :
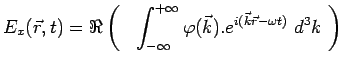 |
où ![]() désigne la partie réelle de la
parenthèse qui suit.
désigne la partie réelle de la
parenthèse qui suit.
Chacune des exponentielles sous le signe d'intégration décrit
une onde plane monochromatique
![]() à laquelle
correspondI13 un état d'impulsion
et donc d'énergie bien définie du photon :
à laquelle
correspondI13 un état d'impulsion
et donc d'énergie bien définie du photon :
La fonction ![]() décrit donc un paquet d'ondes planes. Si le champ (et donc
le photon) est polarisé dans une direction fixe
décrit donc un paquet d'ondes planes. Si le champ (et donc
le photon) est polarisé dans une direction fixe
![]() :
:
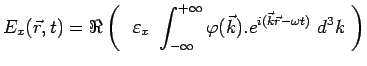 |
de telle sorte qu'avec la correspondance :
 |
le paquet d'ondes classiques est transposé en une superposition quantique :
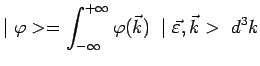 |
ou encore plus généralement, si l'état de polarisation
![]() est lui-même décomposé en la somme vectorielle de deux états de base de
polarisation
est lui-même décomposé en la somme vectorielle de deux états de base de
polarisation
![]() et
et
![]() :
:
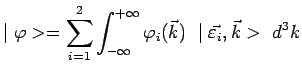 |
On remarque que le nombre de vecteurs de base indépendants
![]() est égal à deux fois
est égal à deux fois ![]() le nombre de valeurs distinctes du triplet
le nombre de valeurs distinctes du triplet
![]() . Or ce
nombre est infini avec la puissance du continu. Plus
généralement il apparaitra ultérieurement qu'il en est de
même pour toute particule, dès lors qu'elle n'est pas
enfermée dans une région limitée de l'espace physique.
. Or ce
nombre est infini avec la puissance du continu. Plus
généralement il apparaitra ultérieurement qu'il en est de
même pour toute particule, dès lors qu'elle n'est pas
enfermée dans une région limitée de l'espace physique.
D'une façon tout à fait générale, quand toutes les
propriétés d'un système physique sont prises en compte, et même
quand il s'agit du système physique le plus simple imaginable (par
exemple une particule comme on vient de le voir) la dimension de
l'espace des états n'est plus dénombrable comme elle doit
l'être pour un espace de Hilbert. Cet espace des états a une
infinité continue de dimensions en même temps que de vecteurs
de base indépendants. Un tel espace est donc une extension
d'espace de Hilbert. Ses vecteurs de base sont alors repérés
par un ou plusieurs indices continus, ![]() ,
, ![]() ,... réels,
comme l'étaient les états d'onde plane
,... réels,
comme l'étaient les états d'onde plane
![]() considérés précédemment,
c'est-à-dire dont les valeurs varient dans des intervalles
(éventuellement
considérés précédemment,
c'est-à-dire dont les valeurs varient dans des intervalles
(éventuellement
![]() ) de telle sorte que :
) de telle sorte que :
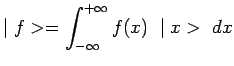 |
ce qui constitue une généralisation de la décomposition habituelle d'un
vecteur sur une base discrète :
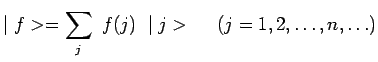 |
et de même que l'on obtient dans le cas d'une telle
base orthonormée
![]() :
:
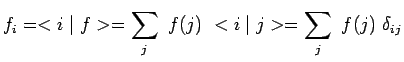 |
il faut pouvoir écrire dans le cas d'une base
continue :
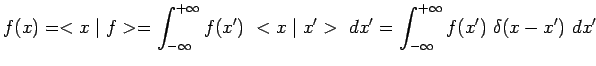 |
avec la notation conventionnelle :
où le second membre, appelé delta de Dirac,
remplace le delta de Kronecker qui apparaît au second membre de
la relation d'orthonormalisation d'une base discrète :
Le delta de Dirac
![]() dépend des deux variables continues
dépend des deux variables continues ![]() et
et ![]() . Toutefois, on peut montrer que ce n'est pas une fonction de ces
deux variables. Il n'existe en effet aucune fonction
. Toutefois, on peut montrer que ce n'est pas une fonction de ces
deux variables. Il n'existe en effet aucune fonction
![]() qui
permette de satisfaire la relation postulée ci-dessus :
qui
permette de satisfaire la relation postulée ci-dessus :
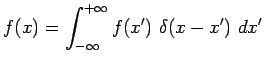 |
Il existe seulement des suites de fonctions ![]() telles que :
telles que :
|
|
Le delta de Dirac représente un nouvel être mathématique dont Dirac a postulé l'existence pour pouvoir assurer la cohérence du formalisme. Les mathématiciens ont ensuite défini et étudié les propriétés de ces nouveaux êtres qui sont aujourd'hui appelés des distributions.
Pour la suite, il suffit de savoir que le delta de Dirac figure toujours sous un
signe d'intégration et qu'il a la signification opérationnelle :
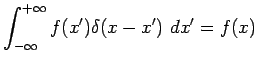 |
quelle que soit ![]() et notamment :
et notamment :
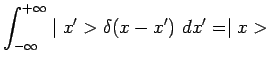 |
Si toutefois, on considère la suite de fonctions
![]() on est
tenté d'écrire en comparant les deux expressions précédentes de
on est
tenté d'écrire en comparant les deux expressions précédentes de ![]() et en admettant à tort que la limite de l'intégrale est égale à
l'intégrale de la limite :
et en admettant à tort que la limite de l'intégrale est égale à
l'intégrale de la limite :
![]() désignant alors une fonction de
désignant alors une fonction de ![]() nulle partout
sauf au point
nulle partout
sauf au point
![]() où sa valeur est infinie, mais pour une telle
fonction, nulle presque partout :
où sa valeur est infinie, mais pour une telle
fonction, nulle presque partout :
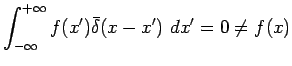 |
Ainsi le delta de Dirac n'est pas une fonction limite des
fonctions
![]() quand
quand
![]() . Ce delta de
Dirac n'a de sens que quand il figure sous un signe
d'intégration, et ce sens est opérationnel : il réalise
immédiatement l'intégration. Toutefois, compte tenu de la
relation entre ce delta de Dirac et la suite des fonctions
. Ce delta de
Dirac n'a de sens que quand il figure sous un signe
d'intégration, et ce sens est opérationnel : il réalise
immédiatement l'intégration. Toutefois, compte tenu de la
relation entre ce delta de Dirac et la suite des fonctions
![]() on peut écrire formellement :
on peut écrire formellement :
Il en résulte donc que les vecteurs kets dépendants d'une base continue ne sont pas normalisables et l'espace vectoriel qu'ils engendrent est donc une extension d'espace de Hilbert et qui resterait à définir mathématiquement.
Nous verrons plus tard que seuls les vecteurs normés ou normalisables peuvent représenter des états physiques. Les vecteurs non normalisables constituent principalement des objets mathématiques utiles mais peuvent correspondre à des états physiques limites et donc inaccessibles.
En effet, il apparaîtra dans la suite qu'un vecteur ket tel que
![]() représente un état physique dans lequel la particule
considérée est localisée parfaitement en un point
mathématique de coordonnées
représente un état physique dans lequel la particule
considérée est localisée parfaitement en un point
mathématique de coordonnées ![]() (
( ![]() désignant globalement
les trois coordonnées spatiales
désignant globalement
les trois coordonnées spatiales ![]() ). Nous savons par
application des relations d'HeisenbergI14que :
). Nous savons par
application des relations d'HeisenbergI14que :
de telle sorte que dans un tel état, s'il pouvait être réalisé,
l'impulsion de cette particule serait totalement indéterminée :
Cependant, à partir de ces vecteurs kets ![]() représentatifs d'états limites inaccessibles, on peut
construire par superposition linéaire des kets
représentatifs d'états limites inaccessibles, on peut
construire par superposition linéaire des kets
![]() représentatifs d'états physiques dans
lesquels nous verrons que la particule est approximativement
localisée soit par exemple dans un intervalle de longueur
représentatifs d'états physiques dans
lesquels nous verrons que la particule est approximativement
localisée soit par exemple dans un intervalle de longueur
![]() aussi petit que l'on veut et centré sur un point de
coordonnées
aussi petit que l'on veut et centré sur un point de
coordonnées ![]() :
:
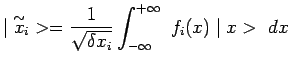 |
![]() désignant une fonction nulle partout sauf
dans l'intervalle
désignant une fonction nulle partout sauf
dans l'intervalle
![]() où sa valeur bornée peut être
quelconque, de telle sorte que si les intervalles
où sa valeur bornée peut être
quelconque, de telle sorte que si les intervalles
![]() sont égaux et couvrent l'axe réel, en se juxtaposant
sont égaux et couvrent l'axe réel, en se juxtaposant
![]() :
:
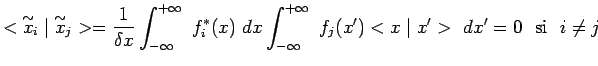 |
Notamment si on choisit une fonction ![]() telle que :
telle que :
on obtient finalement :
et on pourrait écrire alors :
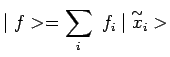 |
Néanmoins il est plus commode d'utiliser les vecteurs kets ![]() non normalisables comme si ils constituaient une base
mathématique et d'utiliser les deltas de Dirac sous des signes
d'intégration en tant qu'outils opérationnels. On notera, par
exemple, la correspondance entre l'expression classique du paquet
d'onde considéré précédemment et sa transposition
quantique. L'état du photon est codé par un ket
non normalisables comme si ils constituaient une base
mathématique et d'utiliser les deltas de Dirac sous des signes
d'intégration en tant qu'outils opérationnels. On notera, par
exemple, la correspondance entre l'expression classique du paquet
d'onde considéré précédemment et sa transposition
quantique. L'état du photon est codé par un ket
![]() normalisé (
normalisé (
![]() ) grâce aux
fonctions
) grâce aux
fonctions
![]() mais les états d'ondes planes qui
ne sont pas réalisables physiquement sont codés par des kets
mais les états d'ondes planes qui
ne sont pas réalisables physiquement sont codés par des kets
![]() non normalisables.
non normalisables.
Question 1-1 : Soit une suite de n vecteurs
![]() supposés normalisables
et linéairement indépendants. En déduire et construire une
base orthonormée de vecteurs
supposés normalisables
et linéairement indépendants. En déduire et construire une
base orthonormée de vecteurs ![]() tels que
tels que
![]()
Question 1-2 : Démontrez que si
![]() alors :
alors :
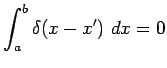 |