Principe de superposition des états

Puisque les états physiques sont représentés par des vecteurs, il en résulte immédiatement les deux conséquences suivantes qui constituent ce qui est appelé le principe de superposition des états :

1- Si un vecteur $\mid \Psi>$ peut s'écrire sous la forme d'une somme de vecteurs kets :

$$\begin{array}{\vert c\vert} \hline { } \\ ~~~\mid \Psi> ~=~ ... ...s_{k=1}^{n}$}~\Psi_k~\mid a_k>~~~ \\ { } \\ \hline \end{array}$$

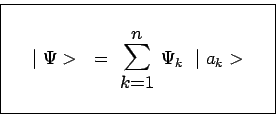le décodage du postulat I impliquera que l'état physique $\Psi$ représenté par le ket $\mid \Psi>$ peut être considéré comme résultant de la superposition des états physiques ``$a_k$ '' représentés par les kets $\mid a_k>$

2- Inversement si un état physique $\Psi$ peut être considéré comme résultant de, ou équivalent à, la superposition d'autres états physiques ``$a_1$ '', ``$a_2$ '',... le ket $\mid \Psi>$ représentatif de l'état $\Psi$ peut s'écrire sous la forme d'une combinaison linéaire des kets $\mid a_k>$ avec $k=1,2,... n$ :

$$\mid \Psi>=\sum\limits_{k=1}^{n}~\Psi_k~\mid a_k>$$

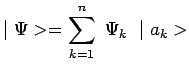Précédemment, nous avons déjà remarqué comment l'état général de la polarisation d'un photon pouvait ainsi se décomposer de multiples façons en une somme de deux états de polarisation rectilignes orthogonaux.

Très prochainement, nous remarquerons qu'une telle décomposition peut faire apparaître une infinité même non dénombrable de composantes.