Le principe de réduction du paquet d'ondes réexaminé

Nous situant toujours dans la perspective du point de vue de Bohr qui écarte toute implication réaliste ou ontologique, nous nous proposons de commenter le principe de réduction du paquet d'ondes. Ce principe se situe dans le prolongement du principe de décomposition spectrale dont il peut apparaître comme une conséquence. Nous rappellerons donc une nouvelle fois ce principe de Bohr.

Si sur un ensemble de

systèmes physiques identiques et indépendants, supposés tous placés dans un même état initial $\Psi$ , codé par le vecteur ket $\mid \Psi>$ normé, on mesure la même grandeur^II21 physique $\hat{A}$ , on trouvera pour résultat de mesure chacune des valeurs propres

(supposées pour simplifier discrètes et non dégénérées) de l'observable

image de $\hat{A}$ , et un nombre de fois égale à

de telle sorte que, avec :

$\displaystyle \mathcal{P}rob~(\hat{A}=a_k)$

$\displaystyle =$

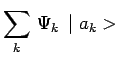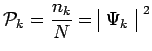$\displaystyle \mathcal{P}_k=\frac{n_k}{N}=\begin{array}{\vert c\vert}\Psi_k\\ \end{array}^{~2}$

Si, par contre, on avait mesuré une grandeur physique $\hat{B}$ autre que $\hat{A}$ , une autre décomposition spectrale :

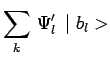aurait indiqué d'autres probabilités $\mathcal{P}^\prime_l$ concernant cette autre mesure :

$\displaystyle \mathcal{P}rob~(\hat{B}=b_l)$

$\displaystyle =$

$\displaystyle \mathcal{P}^\prime_l=\begin{array}{\vert c\vert}\Psi^\prime_l\\ \end{array}^{~2}$

ces nouvelles probabilités n'ayant d'ailleurs de sens, que si la grandeur $\hat{B}$ est effectivement mesurée.

On peut encore considérer, par la pensée, l'un quelconque de ces systèmes indiscernables. Ce système unique est alors représentatif de l'ensemble et son état $\Psi$ codé par le vecteur ket $\mid \Psi>$ est le catalogue des probabilités considérées ci-dessus : $\mathcal{P}_k$ ou $\mathcal{P}^\prime_l\ldots$ etc et dont chacune des pages correspond à chacune des observables :

(ou chacune des E.C.O.C.) qui peuvent être mesurées.

Tant que les mesures des grandeurs $\hat{A}$ et $\hat{B}$ n'ont pas été effectuées, les probabilités $\mathcal{P}_k$ ou $\mathcal{P}^\prime_l\ldots$ n'indiquent pas avec quelle probabilités le système étudié se trouve déjà dans l'état codé $\mid a_k>$ ou dans l'état codé $\mid b_l>$ mais indiquent seulement les probabilités d'y trouver le système, si la grandeur $\hat{A}$ ou si la grandeur $\hat{B}$ est effectivement mesurée. De ces remarques il résulte que le concept d'état et sa représentation par un vecteur ket constituent seulement les outils opérationnels du formalisme. Les probabilités sont mesurables expérimentalement. Ni l'état, ni son vecteur ket image ne le sont.

De ces remarques se dégage une conception du réel bien éloignée de celle suggérée par l'expérience immédiate et ensuite structurée par la mécanique et la physique classiques. Selon ces dernières toute mesure idéale ne fait que constater un état de chose qui existe indépendamment de son observation.

Au contraire, selon la physique quantique, le système étudié ne possède réellement une propriété dynamique déterminée qu'à partir du moment où cette propriété a été observée. Un tel point de vue se situe dans le prolongement de celui de la théorie de la relativité restreinte, selon laquelle le réel est constitué d'événements, c'est-à-dire de phénomènes observés qui sont constitués de coïncidences spatio-temporelles. Mais alors, se demander, dans l'expérience des deux fentes de Young, par laquelle des deux fentes est passé le photon, quand rien dans l'appareillage ne permet de le savoir, c'est en fait se demander où s'est passé un événement qui n'a pas eu lieu, puisqu'il n'a donné lieu à aucune sorte de manifestation.

Si donc une variable dynamique (position, impulsion, énergie ... etc) n'a pas de valeur déterminée avant d'être mesurée, la mesurer ne peut pas signifier : trouver la valeur qu'elle a ! Donc comme l'écrit Schrödinger^II22 :

$~~~\ll$ Si ce n'est pas la réalité qui détermine le résultat de la mesure, c'est donc au moins le résultat de la mesure qui détermine la réalité. $\gg$

Le résultat de la mesure doit donc exister après la mesure, c'est-à-dire que si on répète immédiatement la même mesure on devra retrouver le même résultat. Une telle conséquence constitue la raison d'être de la mesure, et explique la définition qu'en donne Schrödinger^II23 :

$~~~\ll$ L'interaction dûment planifiée entre deux systèmes (l'objet mesuré et l'instrument de mesure) constitue une mesure pour le premier système si une caractéristique variable, et directement accessible aux sens, du second (par exemple la position d'une aiguille) se répète exactement -- dans les limites des erreurs inhérentes à la mesure -- lorsqu'on répète immédiatement le même processus sur le même objet mesuré, sous réserve que celui-ci n'ait pas été soumis à d'autres influences entretemps. $\gg$

Un tel énoncé exprime le contenu essentiel du principe de réduction du paquet d'ondes dont le mécanisme peut être décomposé en deux étapes : $\imath-$ Passage de l'état pur au mélange

En effet, si, comme il vient d'être dit, suite à une première mesure d'une observable

, le résultat obtenu, soit par exemple $\hat{A}=a_k$ , doit être nécessairement répété identiquement, lors d'une deuxième mesure de $\hat{A}$ immédiatement consécutive, il résulte alors du formalisme et notamment d'une conséquence^II24 du postulat III que l'état $\Psi$ du système consécutif à la première mesure doit être représenté par le ket propre $\mid a_k>$ correspondant à la valeur propre

de l'observable

Des deux postulats III et IV ainsi associés, il résulte alors que si la mesure de la grandeur $\hat{A}$ , codée par l'observable

, portait sur un ensemble de

systèmes identiques, indépendants et tous supposés placés dans un même état initial codé par le vecteur normé $\mid \Psi>$ , cette mesure a pour effet de décomposer cet ensemble en une partition, telle qu'à chacune des valeurs propres

corresponde un sous-ensemble réunissant

systèmes placés dans le même état final codé $\mid a_k>$ avec :

Puisque les systèmes considérés sont indiscernables, il est sans signification de chercher à les identifier dans l'état final et si, par la pensée, on considère l'un quelconque d'entre eux, on sait seulement que son état consécutif à la mesure est l'un des états codé $\mid a_k>$ avec la probabilité $\mathcal{P}_k$ .

La mesure a donc eu pour effet de transformer l'état pur initial codé par le vecteur ket $\mid \Psi>$ en un mélange codé par l'opérateur densité :

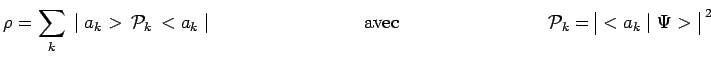$\displaystyle \rho=\sum\limits_k\,\mid a_k>\,\mathcal{P}_k\,<a_k\mid ~~~~~~~~~~... ...~~~~~\mathcal{P}_k=\begin{array}{\vert c\vert}<a_k\mid \Psi>\\ \end{array}^{~2}$

On remarquera que la réalisation de cette première étape n'exige pas que l'expérimenta-teur ou l'observateur prenne immédiatement ou effectivement connaissance du, ou des, résultats obtenus. Il suffit, mais il est aussi nécessaire, que l'appareillage macrosopique de mesure, extérieur au système mesuré, soit tel que, d'une manière ou d'une autre, ces résultats de mesure puissent être connus, soit d'une manière différée soit au moins en principe.

C'est ainsi que, par exemple, si seulement l'une des deux fentes de l'expérience de Young était parfaitement surveillée, le phénomène d'interférence ne se produirait pas, bien qu'aucune détection effective n'ait été faite sur l'autre fente. C'est seulement une sorte de raisonnement logique qui fait localiser les photons sur cette deuxième fente quand ils ne sont pas détectés au passage de la première.

On notera que le phénomène d'interférence disparaitrait également si la détection du passage des particules à travers les fentes était seulement enregistrée sans même qu'il soit pris connaissance ensuite de ces enregistrements.

Rappelons également ici l'expérience déjà décrite, au cours de laquelle des neutrons monocinétiques de faible énergie sont diffractés par un cristal constitué de noyaux de spin $\frac{1}{2}$ . Aux pics de diffraction dûs à la diffusion cohérente, s'ajoute un fond continu dû à une diffusion incohérente. Les neutrons responsables de celle-ci constituent un mélange d'états dont chacun a été localisé par le noyau sur lequel l'interaction a provoqué le renversement du spin. Bien entendu une telle localisation est techniquement inobservable. Ce qui importe seulement, c'est que celle-ci soit théoriquement possible.

Plus généralement, la réalisation de la première étape du processus de réduction du paquet d'ondes exige seulement que l'interaction liée à la mesure ait laissé des traces irréductibles et qu'ainsi le résulat de la mesure soit enregistré d'une manière irréversible dans et par un appareillage macrosopique.

Cette première étape du processus semble objective puisque l'observateur conscient en parait absent. Le croire serait illusoire car les notions d'appareillage macrosopique et d'irréver-sibilité sont implicitement mais intimement liées à celle d'observateur conscient.

Néanmoins, certaines études relativement récentes tendent à laisser croire que la prise en compte rigoureuse de l'interaction inévitable du système observé, quand il est macroscopique, avec son environnement tellement complexe pourrait suffire pour expliquer le passage de ce système à l'état de mélange (processus de décohérence). Ainsi pourrait-on réconcilier un monde macroscopique classique et sa sous-structure microscopique et quantique.

Par exemple, en ce qui concerne le paradoxe du chat de Schrödinger, le dispositif expéri-mental, pourrait-on dire, inscrit lui-même en permanence et d'une manière irréversible la situation effective du chat : mort ou vivant. Autrement dit, le chat serait en état d'observation permanente^II25. Un tel point de vue réaliste n'est pas celui de l'école de Copenhague.

L'étape précédente qui vient d'être analysée est à la foi capitale et paradoxale. En effet, c'est au cours de cette étape que s'est manifesté le caractère indéterministe propre aux phénomènes quantiques. Le même état pur initial a en effet donné naissance à un mélange d'états fondamentalement différents puisque les vecteurs qui les représentent sont orthogonaux. Par contre la probabilité $\mathcal{P}_k$ qui affecte chacun de ces états $\mid a_k>$ dans le mélange est une probabilité de type classique puisqu'elle résulte seulement de l'ignorance de l'observateur. Il lui suffit de lire le résultat enregistré dans l'appareil de mesure, par exemple $\hat{A}=a_l$ , pour en déduire comment représenter l'état final correspondant de ce système observé : $\mid a_l>$ .

Si au lieu d'étudier un seul système physique, on considère un ensemble de

systèmes identiques il est curieux de constater que c'est au contraire la première étape qui parait déterministe et la seconde aléatoire.

En effet, un tel ensemble constitue en fait un système macroscopique sur lequel on mesure des valeurs moyennes, de telle sorte que la valeur moyenne de l'observable

par exemple, est parfaitement déterminée par l'opérateur densité $\rho_i$ de ce système :

C'est ainsi que la figure d'interférence de l'expérience des deux fentes de Young était parfaitement compatible avec le déterminisme classique.

Au contraire, la deuxième étape du processus de la mesure ne met alors en jeu qu'un seul système individuel (par exemple observation du point d'impact d'un photon sur une frange d'interférence). L'observateur repère le résultat unique obtenu ``

'' et en déduit l'état final réalisé $\mid a_k>$ pour ce système individuel. Tout se passe alors comme si son état final résultait d'une projection de son état initial dans le sous-espace ${\mathcal{H}}_{a_k}$ associé à la valeur propre ``

'' qui a été aléatoirement trouvée. C'est pour ce système individuel qu'il y a eu alors réduction du paquet d'ondes et c'est ici que se manifeste le comportement fondamentalement indéterministe des systèmes microscopiques individuels et donc l'aspect indéterministe de la mécanique quantique.