

suivant: Interférence coulombienne-nucléaire
monter: Illustrations
précédent: b) Etude quantique
Table des matières
|
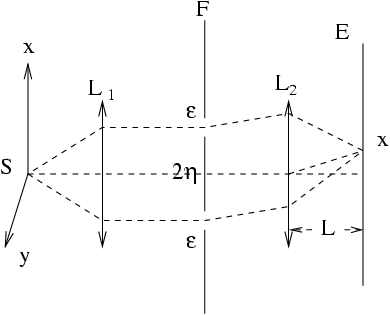
Supposons maintenant que les particules émises par la source
 traversent une feuille
traversent une feuille  percée de deux fentes
horizontales identiques à celles du problème précédent.
Ici encore on se limitera à l'étude des phénomènes dans le
plan de figure
percée de deux fentes
horizontales identiques à celles du problème précédent.
Ici encore on se limitera à l'étude des phénomènes dans le
plan de figure 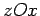 . Comme précédemment, la traversée de la
feuille
. Comme précédemment, la traversée de la
feuille 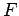 provoque la réduction du paquet d'ondes sur la
composante relative au sous-espace en
provoque la réduction du paquet d'ondes sur la
composante relative au sous-espace en 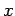 de telle sorte
qu'après cette réduction, cette composante du vecteur ket
représentatif de l'état de la particule s'écrit
approximativement :
de telle sorte
qu'après cette réduction, cette composante du vecteur ket
représentatif de l'état de la particule s'écrit
approximativement :
|
|
La distribution correspondante en impulsion s'en déduit :
soit explicitement :
Or, à une impulsion 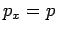 correspond une direction
correspond une direction 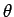 de diffraction et un point d'ordonnée
de diffraction et un point d'ordonnée 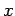 sur
l'écran
sur
l'écran 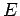 avec :
avec :
d'où :
On peut alors écrire approximativement :
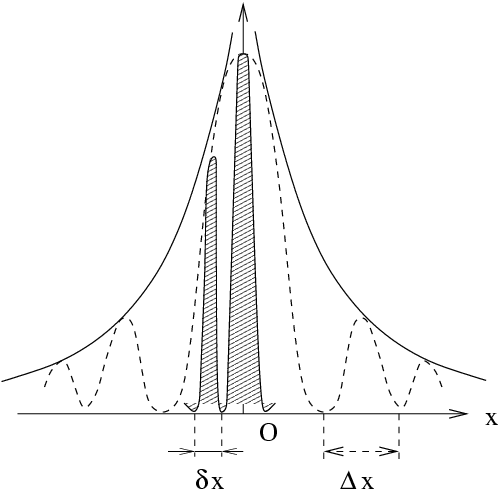
La distribution en intensité de la tache d'interférence s'écrit alors :
La tache de diffraction présente des maxima séparés par des intervalles :
Cette tache est hachée par des franges d'interférences séparées par des intervalles :
Les observations expérimentales sont bien conformes à ces
prévisions théoriques (avec
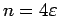 ), comme
l'illustre la figure ci-dessous :
), comme
l'illustre la figure ci-dessous :



suivant: Interférence coulombienne-nucléaire
monter: Illustrations
précédent: b) Etude quantique
Table des matières
Arnaud Balandras
2005-04-02
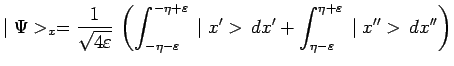
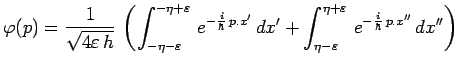
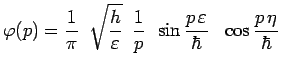
![]() correspond une direction
correspond une direction ![]() de diffraction et un point d'ordonnée
de diffraction et un point d'ordonnée ![]() sur
l'écran
sur
l'écran ![]() avec :
avec :
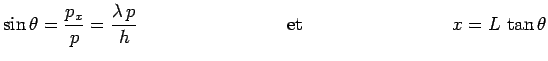

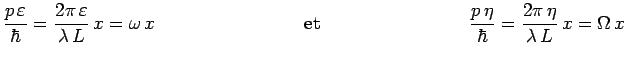
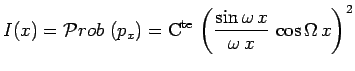
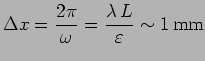
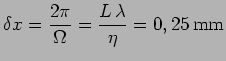
![]() ), comme
l'illustre la figure ci-dessous :
), comme
l'illustre la figure ci-dessous :