Mécanique de Lagrange

A chaque instant $t$ , l'état d'un système mécanique classique peut être caractérisé par les valeurs prises, à cet instant $t$ , par ses coordonnées généralisées (par exemple, les coordonnées de ses particules) notées $q_i$ ( $i=1,2,\ldots,n$ ) et ses vitesses généralisées (par exemple les coordonnées des vitesses de ses particules) notées $\dot{q}_i$ .

A ce système peut être associé une fonction caractéristique de ce système, appelée sa fonction^III1 de Lagrange $\mathcal{L}$ et fonction des variables $q_i$ et $\dot{q}_i$ et éventuellement du temps $t$ :

$$\mathcal{L}=\mathcal{L}(q_i,\dot{q}_i,t)~~~~~(i=1,2,\ldots,n)$$

$n$ étant le nombre de degrés de liberté du système.

A chaque coordonnée $q_i$ on peut associer son moment canoniquement conjugué, noté $p_i$ et défini par :

$$p_i={{\partial\mathcal{L}}\over{\partial\dot{q}_i}}= p_i(q_m,p_m)~~~~~(m=1,2,\ldots,n)$$

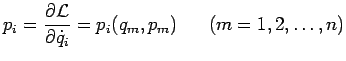Toutes les variables dynamiques classiques d'un système, étant fonctions des variables $q_i$ et $\dot{q}_j$ , peuvent alors s'exprimer en fonction des variables $q_i$ et $p_j$ .