A tout couple de variables dynamiques ![]() et
et ![]() fonctions des
fonctions des ![]() et des
et des
![]() , on peut associer la fonction, appelée crochet de Poisson :
, on peut associer la fonction, appelée crochet de Poisson :
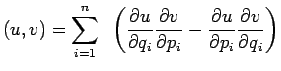 |
et on démontre que ce crochet ![]() est une forme invariante dans
un changement de coordonnées et de moments conjugués.
est une forme invariante dans
un changement de coordonnées et de moments conjugués.
Question 3-1 : Soit une particule de masse ![]() soumise à des forces
qui dérivent d'une fonction potentielle
soumise à des forces
qui dérivent d'une fonction potentielle ![]() .
.
![]() Ecrivez sa fonction de Lagrange
Ecrivez sa fonction de Lagrange
![]() .
.
![]() Exprimez les moments conjugués
Exprimez les moments conjugués ![]() de ses coordonnées
de ses coordonnées
![]() .
.
![]() Exprimez en fonction des
Exprimez en fonction des ![]() et des
et des ![]() la fonction
la fonction
![]() énergie totale et les composantes de son moment cinétique
énergie totale et les composantes de son moment cinétique ![]() à l'origine.
à l'origine.
![]() Calculer les crochets de Poisson :
Calculer les crochets de Poisson :
![]()
Les principales propriétés des crochets de Poisson résultent de leur définition :
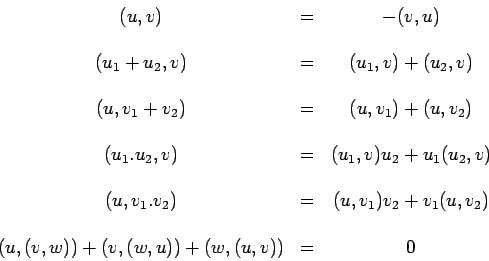 |
On notera que dans les quatrième et cinquième relations, on a respecté
dans l'écriture des seconds membres l'ordre des facteurs ![]() et
et ![]() d'une
part, et
d'une
part, et ![]() et
et ![]() d'autre part. Cet ordre est sans importance dans la
mécanique classique, mais va devenir essentiel dans la mécanique quantique, comme il
apparait ci-après.
d'autre part. Cet ordre est sans importance dans la
mécanique classique, mais va devenir essentiel dans la mécanique quantique, comme il
apparait ci-après.