Nous avons déjà vuIII7 que, dans un espace
à une dimension, l'état d'une particule codé par le vecteur
ket ![]() admet notamment les deux représentations
particulières suivantes :
admet notamment les deux représentations
particulières suivantes :
Les deux fonctions d'ondes ![]() et
et
![]() se déduisent l'une de
l'autre :
se déduisent l'une de
l'autre :
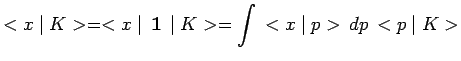 |
et :
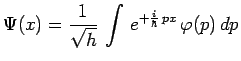 |
ou encore symétriquement :
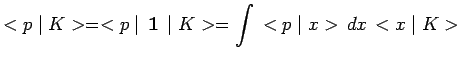 |
et :
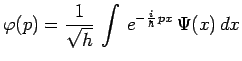 |
sachant que, comme il sera démontré
ultérieurementIII8 :
Les fonctions
![]() et
et ![]() sont donc transformées de Fourier
l'une de l'autre. D'un théorème de mathématique, il résulte alors que
les écarts-types des variables
sont donc transformées de Fourier
l'une de l'autre. D'un théorème de mathématique, il résulte alors que
les écarts-types des variables ![]() et
et ![]() satisfont toujours l'inégalité
mathématique :
satisfont toujours l'inégalité
mathématique :
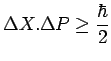 |
qui n'est autre que l'une des inégalités de Heisenberg.
C'est ce que nous allons vérifier dans le cas particulier d'un état ![]() dans lequel la particule est approximativement localisée dans le voisinage
dans lequel la particule est approximativement localisée dans le voisinage
![]() d'un point que nous choisirons pour origine :
d'un point que nous choisirons pour origine :
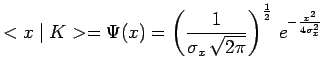 |
On vérifie en effet :
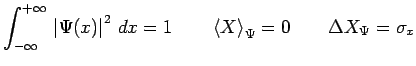 |
De ce qui précède résulte que ce même état ![]() peut encore s'écrire
:
peut encore s'écrire
:
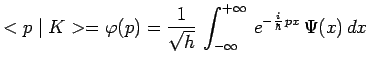 |
soit explicitement, après substitution de la fonction ![]() et
intégration :
et
intégration :
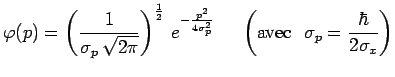 |
On notera la similitude de cette expression avec la précédente, d'où
résulte immédiatement :
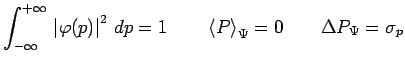 |
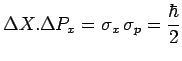 |
Nous nous trouvons dans le cas particulier où l'inégalité de Heisenberg devient une égalité.
Le résultat qui vient d'être obtenu :
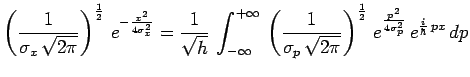 |
est une illustration de la relation générale :
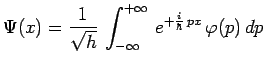 |
dans le cas particulier d'une fonction
![]() gaussienne.
gaussienne.
Question 3-7 : Considérez le cas d'une fonction
![]() normalisée, nulle partout sauf si
normalisée, nulle partout sauf si
![]() et égale à
et égale à
![]() si
si
![]() , où
, où ![]() désigne un
intervalle centré sur une valeur
désigne un
intervalle centré sur une valeur ![]() .
.
|
|
![]() Montrez que la fonction d'onde de Schrödinger de cet état
s'écrit :
Montrez que la fonction d'onde de Schrödinger de cet état
s'écrit :
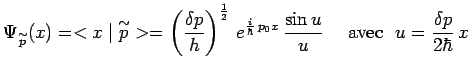 |
![]() Montrez qu'elle est bien normalisée. Calculez
Montrez qu'elle est bien normalisée. Calculez
![]() ,
,
![]() et
et ![]() .
.
|
|
Question 3-8 : En considérant seulement la dimension ``![]() '' du
problème, montrez qu'à la sortie du trou l'état initial d'impulsion
'' du
problème, montrez qu'à la sortie du trou l'état initial d'impulsion
![]() devient, après réduction du paquet d'ondes :
devient, après réduction du paquet d'ondes :
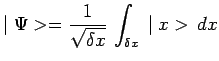 |
![]() désignant la largeur du trou. Déterminez la
distribution en impulsion des particules sortantes en calculant la fonction de
probabilité :
désignant la largeur du trou. Déterminez la
distribution en impulsion des particules sortantes en calculant la fonction de
probabilité :
Tracez la courbe représentative de la fonction densité de
probabilité
![]()
Bien évidemment, tous les résultats précédents peuvent être
immédiatement généralisés au cas de l'espace physique à trois dimensions,
et par exemple avec :
 |