Remarque

Les valeurs des dispersions indiquées dans ce tableau révèlent à nouveau combien les états propres, dépendant d'un spectre continu, sont irréalisables expérimentalement. Ce sont seulement des états limites, dont on peut éventuellement se rapprocher, sans jamais les atteindre.

Il ne faut pas imaginer que dans son état , la particule aurait réllement en fait une position et une impulsion bien déterminées, mais cachées, et que et seraient les erreurs possibles commises en mesurant et , de telle sorte que les résultats de mesure seraient alors affectés des incertitudes et . L'imaginer reviendrait à considérer la particule comme une chose en soi, dotée de propriétés intrinsèques plus ou moins accessibles à la mesure.

L'inégalité de Heisenberg implique que dans un état quelconque, la particule n'a ni une position , ni une impulsion bien déterminées. Plus est déterminée, moins l'est, et réciproquement.

Ainsi la position et l'impulsion sont deux propriétés incompatibles, que la particule ne peut possèder en même temps. Les concepts de position et d'impulsion sont des concepts classiques correspondant à des propriétés qui ne peuvent être attribuées aux objets quantiques, qu'au prix d'une certaine approximation, c'est-à-dire d'une certaine imprécision. Ce sont également des concepts limites, en ce sens, que dans ces états limites, par exemple , les propriétés correspondantes à certains de ces concepts, par exemple , peuvent être attribués à la particule, mais alors les propriétés correspondantes, à d'autres concepts complémentaires perdent toute signification : . Les inégalités de Heisenberg délimitent le domaine de validité de ces concepts classiques. Elles nous permettent de savoir dans quelle mesure ils sont significatifs.

La notion classique de trajectoire suppose qu'à chaque instant la particule possède une postion et une impulsion déterminées. De ce qui précède, il résulte qu'une telle notion ne peut être conservée telle quelle en mécanique quantique. PrécédemmentIII6(orbites de Bohr, interférences à un photon, diffraction d'un photon par une fente,... etc) nous n'avons cessé de constater combien cette notion classique de trajectoire semblait peu explicative, et combien au contraire, elle conduisait à des paradoxes insolubles quand on persistait à l'utiliser.

Et pourtant, dans une chambre à bulles par exemple, ne prétend on pas photographier la trajectoire d'une particule ? En fait, on photographie seulement un chapelet de bulles, auxquelles correspondent autant de mesures de position etc, faites à des instants successifs séparés par un intervalle moyen de temps .   En modifiant certains paramètres expérimentaux, on peut dans une certaine mesure augmenter la densité et réduire la grosseur de ces bulles, ce qui revient à réduire , et donc, en particulier l'intervalle de temps qui sépare la localisation en à l'instant et la localisation en à l'instant .

La mécanique classique prétend que lorsque , le point dont la position dépend de , soit , se rapproche de :

en se déplaçant sur une courbe continue qui est la trajectoire, de telle sorte que la fonction admet une dérivée à l'instant qui est la vitesse instantanée :

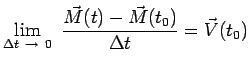Au contraire, la mécanique quantique prévoit que si on pouvait faire des mesures successives de position pour des valeurs décroissantes de :

on trouverait des localisations successives aléatoires :

et probablement situées dans un élément de volume de plus en plus petit autour de , mais sans venir s'aligner sur une courbe continue.

Autrement dit, la fonction est bien une fonction aléatoire continue, mais sans dérivée. Ainsi une particule microscopique n'a pas de trajectoire. La mécanique quantique renonce à cette idée d'une évolution continue dans l'espace, au cours du temps, telle qu'elle était admise par la mécanique classique, au vu des observations macroscopiques.