b) Induites

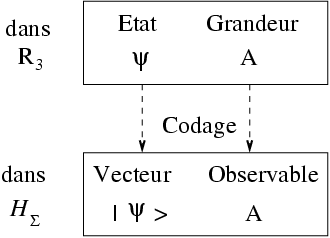
Conformément au codage mathématique défini pa la mécanique quantique, toute transformation $T$ effectuée dans l'espace physique $\mathbf{R}_3$ sur le système $\Sigma$ , ses états $\Psi$ ou les appareils qui mesurent ses grandeurs physique s $\hat{A}$ , est représentée par un opérateur image $\mathcal{T}$ agissant dans l'espace $\cal{H}_{\cal{\Sigma}}$ des vecteurs kets de telle sorte que : $$\mathrm{Si}~~~\Psi^\prime=T\,\Psi~~~~~~\mathrm{alors}~~~~~~ \mid \Psi^\prime>=\mathcal{T}\,\mid \Psi>$$    Toute transformation telle que $\mathcal{T}$ est appelée transformation induite par $T$ .

Tout état défini du système est réalisé au moyen d'un appareillage, qui a pour effet de placer le système dans cet état. Une telle réalisation s'appelle aussi une préparation. Déplacer l'état du système, par exemple dans la direction $O\vec{x}$ et d'une distance $\delta x$ , c'est donc déplacer cet appareillage dans la direction $O\vec{x}$ et d'une distance $\delta x$ . De même déplacer une observable, c'est déplacer l'appareillage correspondant à la mesure de cette observable.

Par exemple, une façon triviale de localiser une particule consiste à l'enfermer dans le volume $V$ intérieur à une boite de telle sorte que :

$$\Psi(\vec{r})=0~~~~~~\mathrm{si}~~~~~~\vec{r}\not\in\,V$$

Déplacer l'état $\Psi$ de cette particule, c'est déplacer cette boite, qui après déplacement occupera un nouveau volume $V^\prime$ de telle sorte que l'état déplacé $\Psi^\prime$ sera tel que :

$$\mid \Psi>~~\longrightarrow~~\mid \Psi^\prime>~~~~~~\mathrm{avec}~~~~~~ \Psi^\prime(\vec{r})=0~~~\mathrm{si}~~~\vec{r}\not\in\,V^\prime$$

De même, faire tourner une grandeur physique dans l'espace, par exemple la composante $z$ du spin d'une particule soit $\hat{S}_z$ , c'est appliquer cette même rotation à l'appareillage (un aimant de Stern et Gerlach) qui permet de mesurer cette grandeur physique. Le nouvel appareillage orienté dans la nouvelle direction $z^\prime$ mesure la nouvelle grandeur physique $\hat{S}_{z^\prime}$ . On dit que la rotation physique $R$ effectuée dans l'espace physique $\mathbf{R}_3$ et appliquée à l'appareillage, a induit dans l'espace $\cal{H}_{\cal{S}}$ des états une rotation induite $\mathcal{R}$ , qui a transformé l'observable $S_z$ en la nouvelle observable $S_{z^\prime}$ . La manière dont $S_{z^\prime}$ résulte de $S_z$ par action de $\mathcal{R}$ va être précisée ci-dessous.

Toutefois, comment définir le vecteur ket correspondant à l'état déplacé ? Cet état détermine seulement la direction de ce ket. Nous précisons cette détermination en postulant que le ket déplacé $\mid \Psi>_d$ a même longueur que le ket $\mid \Psi>$ et donc demeure encore défini à un facteur de phase près $e^{i\alpha}$ ($\alpha$ réel) qui pourrait dépendre du ket considéré ou même demeurer arbitraire. Plus généralement, il y a lieu de rappeler ici que tout opérateur de transformation doit respecter le principe de superposition des états, et donc :

$$\mathrm{Si}~~~~~~ \mid \Psi>=\alpha\,\mid \varphi>+\beta\,\mid \c... ...\mathrm{il~faut}~~~~~~ \mid \Psi>_d=\alpha\,\mid \varphi>_d+\beta\,\mid \chi>_d$$

c'est-à-dire :

$$\mid \Psi>_d=\mathcal{T}\,\mid \Psi>= \mathcal{T}\,\left(\alpha\,... ...hi>\right)= \alpha\,\mathcal{T}\,\mid \varphi>+\beta\,\mathcal{T}\,\mid \chi>\$$

Ainsi $\mathcal{T}$ est un opérateur linéaire défini à un facteur de phase près $e^{i\alpha}$ arbitraire, mais constant et indépendant du vecteur auquel $\mathcal{T}$ est appliqué (changement de jauge global).

La loi de transformation des opérateurs se déduit de celle des vecteurs kets. En effet, le transformé $\Omega_d$ d'un opérateur $\Omega$ est défini par :

$$\mathrm{Si}~~~~~~ \mid \Psi>=\Omega\,\mid \varphi>~~~~~~~~~~~~\mid \Psi>_d=\Omega_d\,\mid \varphi>_d$$

$$\mathrm{Soit}~~~~~~ \mathcal{T}\,\mid \Psi>=\mathcal{T}\,\Omega\,\mid \varphi>=\Omega_d\,\mathcal{T}\,\mid \varphi>$$

et puisque $\mid \varphi>~\in~\mathcal{H}$ est quelconque :

$$\fbox{$\Omega_d=\mathcal{T}\,\Omega\,\mathcal{T}^{-1}$}$$

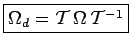Une telle loi de transformation des opérateurs $\Omega$ sous l'effet de l'opérateur $\mathcal{T}$ s'appelle une transformation de similarité.