Du point de vue de la physique classique, déplacer par translation un système (une
particule par exemple) d'une longueur ![]() c'est amener au point
c'est amener au point
![]() tout élément du système, qui était au point
tout élément du système, qui était au point ![]() .
.
D'un point de vue quantique, cette définition est inadaptée, puisque les objets quantiques ne sont pas supposés tous localisés. Par ailleurs, le formalisme quantique est fondé sur la notion d'état. Déplacer un système consistera donc à déplacer son état.
Or, dans la représentation de Schrödinger, l'état ![]() d'une particule :
d'une particule :
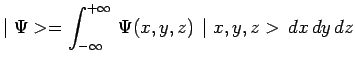 |
peut être représenté par sa fonction d'onde :
qui distribue dans tout l'espace la probabilité de l'y localiser.
Dépacer la particule, c'est donc changer la fonction d'onde représentative de
son état :
Si
![]() désigne l'opérateur correspondant à un
déplacement de longueur
désigne l'opérateur correspondant à un
déplacement de longueur ![]() dans la direction
dans la direction ![]() , on obtient
successivement :
, on obtient
successivement :
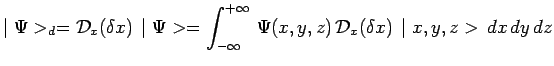 |
mais :
d'où l'expression de l'opérateur de déplacement :
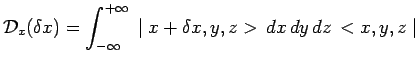 |
et le ket de l'état déplacé devient :
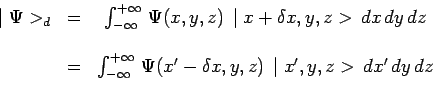 |
en changeant la variable d'intégration
![]() , d'où
résulte la fonction d'onde représentative de cet état déplacé :
, d'où
résulte la fonction d'onde représentative de cet état déplacé :
ou encore plus généralement pour un déplacement
![]() queconque :
queconque :
Considérons tout d'abord des translations de longueur infinitésimale et donc
proches de l'identité :
A l'instar de
![]() ,
, ![]() est un opérateur. Nous verrons comment sa
détermination entraine celle de tous les opérateurs
est un opérateur. Nous verrons comment sa
détermination entraine celle de tous les opérateurs
![]() . Pour
cette raison, on l'appelle le générateur infinitésimal des translations
dans la direction
. Pour
cette raison, on l'appelle le générateur infinitésimal des translations
dans la direction ![]() :
:
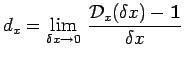 |
![]() est en général défini, comme tout opérateur
est en général défini, comme tout opérateur
![]() de transformation, à un facteur de phase arbitraire près
de transformation, à un facteur de phase arbitraire près
![]() ,
tel que
,
tel que
![]() quand
quand
![]() puisque alors
puisque alors
![]() . Si donc on multiplie
. Si donc on multiplie
![]() par un tel
facteur arbitraire :
par un tel
facteur arbitraire :
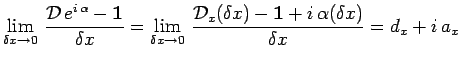 |
![]() désignant un nombre réel, de telle sorte que le
générateur
désignant un nombre réel, de telle sorte que le
générateur ![]() est lui-même défini à une constante imaginaire pure
est lui-même défini à une constante imaginaire pure
![]() additive près.
additive près.
De l'unitarité de
![]() résulte :
résulte :
d'où résulte, puisque ![]() est infinitésimal :
est infinitésimal :
Le générateur ![]() est un opérateur antihermitique.
est un opérateur antihermitique.