Pour un système physique, un atome par exemple, isolé dans
l'espace, toutes les directions de l'espace sont équivalentes.
Plus précisément l'expression de son hamiltonien ![]() est
invariante par rotation, de telle sorte que :
est
invariante par rotation, de telle sorte que :
| 0 |
![]() désignant le moment angulaire total du
système. Tenu compte de l'expression générale d'un
opérateur de rotation induite quelconque :
désignant le moment angulaire total du
système. Tenu compte de l'expression générale d'un
opérateur de rotation induite quelconque :
![]() désignant un axe de rotation quelconque et
désignant un axe de rotation quelconque et
![]() un angle quelconque, il en résulte :
un angle quelconque, il en résulte :
| 0 |
Si donc
![]() désigne un des états de l'atome
correspondant à la valeur propre
désigne un des états de l'atome
correspondant à la valeur propre ![]() :
:
on en déduit immédiatement :
Tous les états
![]() déduits de
déduits de
![]() par une rotation quelconque
par une rotation quelconque
![]() sont donc
également de états propres de
sont donc
également de états propres de ![]() avec la même valeur
propre
avec la même valeur
propre ![]() . Cette valeur propre est donc dégénérée à
moins que l'état
. Cette valeur propre est donc dégénérée à
moins que l'état
![]() ne soit lui-même invariant par
rotation quand :
ne soit lui-même invariant par
rotation quand :
Ainsi en général toute valeur propre de ![]() est
dégénérée et cette dégénérescence, qui résulte de
l'isotropie de l'espace pour le système physique, s'appelle la
dégénérescence de rotation.
est
dégénérée et cette dégénérescence, qui résulte de
l'isotropie de l'espace pour le système physique, s'appelle la
dégénérescence de rotation.
Cette dégénérescence révèle que ![]() ne constitue pas
un E.C.O.C. à lui seul mais puisque :
ne constitue pas
un E.C.O.C. à lui seul mais puisque :
les trois observables
![]() et
et ![]() constituent en général un E.C.O.C. dont les vecteurs propres
communs notés
constituent en général un E.C.O.C. dont les vecteurs propres
communs notés
![]() sont définis sans ambiguïté,
de telle sorte que, en particulier :
sont définis sans ambiguïté,
de telle sorte que, en particulier :
La dégénérescence de la valeur propre ![]() est égale au
nombre de vecteurs propres distincts
est égale au
nombre de vecteurs propres distincts
![]() relatifs à
cette même valeur propre
relatifs à
cette même valeur propre ![]() . En effet, ces vecteurs sont
bien indépendants puisqu'ils sont orthogonaux tandis que les
vecteurs
. En effet, ces vecteurs sont
bien indépendants puisqu'ils sont orthogonaux tandis que les
vecteurs
![]() considérés
précédemment ne l'étaient pas.
considérés
précédemment ne l'étaient pas.
Ces vecteurs propres indépendants se déduisent les uns des
autres par action des opérateurs échelons ![]() et
et ![]() . En
effet puisque
. En
effet puisque ![]() commute avec
commute avec ![]() et
et ![]() :
:
et avec
![]() :
:
La dégénérescence de la valeur propre ![]() est donc égale
au nombre de valeurs distinctes de
est donc égale
au nombre de valeurs distinctes de ![]() , soit
, soit ![]() . Pour chacune
des valeurs propres
. Pour chacune
des valeurs propres ![]() la dégénérescence de rotation
est donc d'ordre
la dégénérescence de rotation
est donc d'ordre
![]() . Elle ne peut être nulle
que si le spin
. Elle ne peut être nulle
que si le spin ![]() de l'état est nul.
de l'état est nul.
La dégénérescence de la valeur propre ![]() pourrait
encore être d'un ordre plus élevé s'il lui correspondait
plusieurs valeurs distinctes de
pourrait
encore être d'un ordre plus élevé s'il lui correspondait
plusieurs valeurs distinctes de ![]() , ce qui constitue toutefois
une circonstance exceptionnelle dûe seulement à la structure
particulièreIII15 du hamiltonien. Ainsi, en général chaque valeur
propre
, ce qui constitue toutefois
une circonstance exceptionnelle dûe seulement à la structure
particulièreIII15 du hamiltonien. Ainsi, en général chaque valeur
propre ![]() ne dépend que des nombres quantiques
ne dépend que des nombres quantiques ![]() et
et ![]() et
ne dépend pas du nombre quantique magnétique ou azimuthal
et
ne dépend pas du nombre quantique magnétique ou azimuthal ![]() :
:
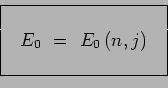 |