Si
![]() et si
et si
![]() , la
particule est libre et l'équation radiale, avec
, la
particule est libre et l'équation radiale, avec
![]() ,
se réduit à :
,
se réduit à :
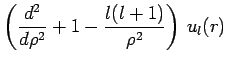 |
0 |
Les solutions régulières et irrégulières à l'origine
sont respectivement
![]() et
et
![]() , où
, où
![]() et
et ![]() désignent respectivement la fonction
de Bessel sphérique et la fonction de Neumann sphérique. On
définit également les fonctions de Hankel sphériques de
désignent respectivement la fonction
de Bessel sphérique et la fonction de Neumann sphérique. On
définit également les fonctions de Hankel sphériques de
![]() et
et
![]() espèce.
espèce.