Nous supposerons :
![]()
![]() borné partout sauf à l'origine en
borné partout sauf à l'origine en ![]() au
plus,
au
plus,
![]()
![]() quand
quand
![]() .
.
La solution générale est une combinaison linéaire de deux
solutions particulières linéaire-ment indépendantes et doit
satisfaire aux conditions de régularité et aux conditions aux
limites pour : ![]() et
et
![]() .
.
Au voisinage de l'origine on trouve une solution du type :
à condition que :
Il existe donc deux solutions correspondant à ![]() et
et ![]() dont seule la première est régulière
dont seule la première est régulière
![]() à l'origine.
à l'origine.
Si
![]() l'équation radiale s'approche de l'équation
:
l'équation radiale s'approche de l'équation
:
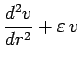 |
0 |
Si
![]() il existe deux solutions indépendantes
régulières à l'infini et qui se comportent comme :
il existe deux solutions indépendantes
régulières à l'infini et qui se comportent comme :
Si
![]() il existe une seule solution
régulière à l'infini qui décroît comme
il existe une seule solution
régulière à l'infini qui décroît comme
![]() et seulement pour certaines
valeurs bien particulières de
et seulement pour certaines
valeurs bien particulières de
![]() .
.
En résumé soit donc la solution ![]() régulière à
l'origine (
régulière à
l'origine (![]() ).
).
Si
![]() elle n'est régulière à l'infini
que pour certaines valeurs de
elle n'est régulière à l'infini
que pour certaines valeurs de
![]() :
:
et se comporte à l'infini comme :
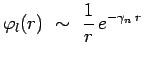 |
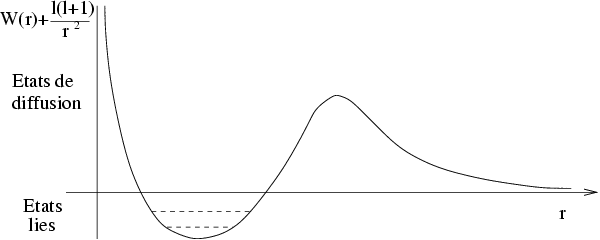
Les états correspondants sont discrets (spectre discret
en énergie) et sont liés (probabilité évanescente
pour ![]() ).
).
Si
![]() la solution
la solution ![]() régulière à
l'origine est toujours également régulière à l'infini et
avec
régulière à
l'origine est toujours également régulière à l'infini et
avec
![]() :
:
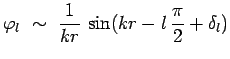 |
avec :
![]() s'appelle le déphasage de l'onde
s'appelle le déphasage de l'onde ![]() , et est dû au
potentiel
, et est dû au
potentiel ![]() . Les états correspondants sont des états non
liés pour lesquels la fonction d'onde ne s'annule pas à
l'infini. Ce sont des états de diffusion. Les fonctions
d'onde correspondantes ne sont pas normalisables au sens strict et
les valeurs propres correspondantes appartiennent au
continuum :
. Les états correspondants sont des états non
liés pour lesquels la fonction d'onde ne s'annule pas à
l'infini. Ce sont des états de diffusion. Les fonctions
d'onde correspondantes ne sont pas normalisables au sens strict et
les valeurs propres correspondantes appartiennent au
continuum :
![]()