Considérons le système constitué d'une seule particule dans l'espace. Nous allons étudier comment varie au cours du temps sa distribution de probabilité de localisation dans l'espace. Autrement dit, sachant que :
avec :
que vaut :
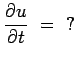
A cet effet, calculons la dérivée de ![]() :
:
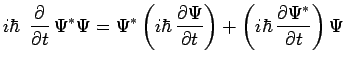 |
Tenu compte de l'équation de Schrödinger :
![$\displaystyle i\hbar~\,{{\partial}\over{\partial t}}\,\Psi=
\left[{{-\hbar^2}\over{2m}}\,\Delta+V(\vec{r})\right]\,\Psi$](img2741.png) |
on obtient :
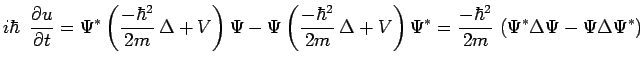 |
Intégrons les deux membres dans un volume ![]() enfermé à
l'intérieur d'une surface
enfermé à
l'intérieur d'une surface ![]() :
:
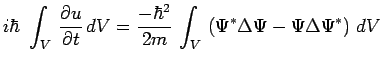 |
ou encore, en utilisant le théorème de Green :
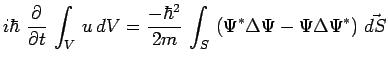 |
Définissons un vecteur
![]() appelé vecteur densité de
courant de probabilité ou simplement vecteur densité de courant tel que :
appelé vecteur densité de
courant de probabilité ou simplement vecteur densité de courant tel que :
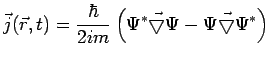 |
De ce qui précède résulte alors :
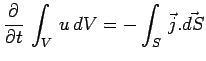 |
|
|
Tenu compte du théorème d'Ostrogradsky, on peut enfin écrire :
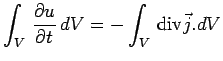 |
Or l'élément de volume ![]() peut être choisi n'importe où, et
arbitrairement petit, de telle sorte qu'en chaque point, et à tout instant :
peut être choisi n'importe où, et
arbitrairement petit, de telle sorte qu'en chaque point, et à tout instant :
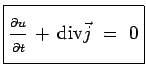 |
Cette dernière équation s'appelle aussi l'équation de continuité. Elle exprime la conservation de la probabilité totale. On notera son analogie mathématique avec l'équation qui exprime la conservation de la charge électrique.
Ainsi, puisque la particule n'est pas localisée à chaque instant dans
l'espace, son état d'évolution ne peut correspondre à une trajectoire,
mais cet état précise comment varie au cours du temps la distribution de sa
probabilité de localisation. Tout se passe comme si l'espace était rempli
par un fluide compressible mais de masse totale bien déterminée et constante
et dont la densité locale :
varie conformément à l'équation de continuité.