Théorèmes d'Ehrenfest

Selon la mécanique classique, dans un état $\Psi$ bien défini et à chaque instant $t$ , chacune des variables dynamiques a également une valeur bien définie. Au contraire, selon la mécanique quantique, aucune de ces variables ou de ces observables n'a de valeur définie en général. Toutefois, à chaque instant $t$ , chacune de ces observables, par exemple $A$ , a une valeur moyenne bien définie :

$$\left<A\right>_\Psi=<\Psi(t)\mid A(t)\mid \Psi(t)>$$

Ci-dessus, l'observable est notée comme si elle était une fonction du temps. Ce cas est exceptionnel, car en général l'expression mathématique des observables telles que :

$$X, ~P_y, ~L_z, ~\ldots ~\mathrm{etc}$$

ne dépend pas du temps. Un tel cas peut néanmoins se produire, par exemple si le système est plongé dans un champ qui dérive d'un potentiel dépendant du temps :

$$V(x,y,z,t)~~~\Longrightarrow~~~V(X,Y,Z,t)$$

Les théorèmes d'Ehrenfest précisent comment varie en fonction du temps la valeur moyenne de chaque observable :

$$\frac{d}{dt}\left<A\right>_\Psi=\frac{d}{dt}<\Psi(t)\mid \,A(t)\m... ...\mid \frac{dA(t)}{dt}\mid \Psi(t)>+<\Psi(t)\mid A(t)\,\frac{d}{dt}\mid \Psi(t)>$$

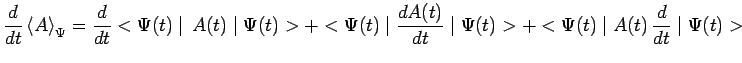Tenu compte de l'équation de Schrödinger :

$$i\hbar\,\frac{d}{dt}\mid \Psi(t)>=H\mid \Psi(t)>~~~~~\mathrm{et}~~~~~ -i\hbar\,\frac{d}{dt}<\Psi(t)\mid =<\Psi(t)\mid H$$

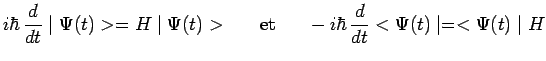on obtient immédiatement l'équation d'Ehrenfest :

$$\begin{array}{\vert ccc\vert} \hline & & \\ ~ & i\hbar\frac{... ...ft<\frac{dA}{dt}\right>_\Psi & ~ \\ & & \\ \hline \end{array}$$

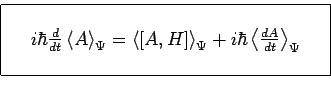On obtient une telle équation pour chaque observable, et, par exemple pour les observables de position et d'impulsion :

$$i\hbar\,\frac{d}{dt}\left<X\right>_\Psi=\left<\left[X,H\right]\right>_\Psi+ \left<\frac{dX}{dt}\right>_\Psi$$

$$i\hbar\,\frac{d}{dt}\left<P_x\right>_\Psi=\left<\left[P_x,H\right]\right>_\Psi+ \left<\frac{dP_x}{dt}\right>_\Psi$$

Il en est de même des autres composantes, de telle sorte que l'on peut noter symboliquement :

$$i\hbar\,\frac{d}{dt}\left<\vec{R}\right>_\Psi=\left<\left[\vec{R},H\right]\right>_\Psi+ \left<\frac{d\vec{R}}{dt}\right>_\Psi$$

$$i\hbar\,\frac{d}{dt}\left<\vec{P}\right>_\Psi=\left<\left[\vec{P},H\right]\right>_\Psi+ \left<\frac{d\vec{P}}{dt}\right>_\Psi$$

Dans le cas particulier d'une particule libre on a :

$$H=\frac{\vec{P}^2}{2m}~~~~~\mathrm{et}~~~~~\left[\vec{P},H\right]=0$$

de telle sorte que la valeur moyenne de l'impulsion satisfait le principe d'inertie de Galilée :

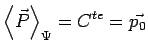$$\left<\vec{P}\right>_\Psi=C^{te}=\vec{p_0}$$