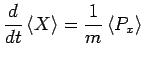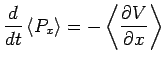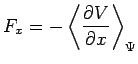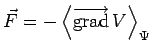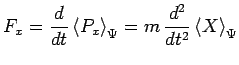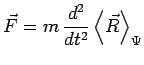


suivant: Remarque
monter: L'approximation classique
précédent: Théorèmes d'Ehrenfest
Table des matières
Si la particule possède également une énergie potentielle, le hamiltonien
s'écrit :
et tenu compte des relations de commutation écrites dans la
représentation de Schrödinger :
Les équations d'Ehrenfest s'écrivent :
Afin d'établir un lien avec la mécanique classique, on peut définir un
vecteur force classique par ses composantes :
soit :
d'où on déduit, à partir des deux équations d'Ehrenfest :
et pour les trois composantes :
Cette équation a bien la forme de l'équation de Newton.
Sous-sections



suivant: Remarque
monter: L'approximation classique
précédent: Théorèmes d'Ehrenfest
Table des matières
Arnaud Balandras
2005-04-02
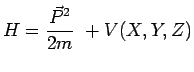
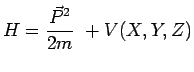
![$\displaystyle \left[X,H\right]=\frac{1}{2m}\left[X,P_x^2\right]=
\frac{1}{2m}\left(P_x\left[X,P_x\right]+\left[X,P_x\right]P_x\right)$](img2838.png)
![$\displaystyle \left[P_x,H\right]=\left[P_x,V\right]=
\frac{\hbar}{i}\,\frac{\partial V}{\partial x}$](img2840.png)