Dans la suite la plupart des opérateurs que nous considèrerons seront hermitiques. Ces opérateurs hermitiques jouissent de propriétés particulières.
![]() Les valeurs propres d'un opérateur hermitique sont
toujours réelles. En effet :
Les valeurs propres d'un opérateur hermitique sont
toujours réelles. En effet :
![]() Deux vecteurs propres
Deux vecteurs propres ![]() et
et ![]() d'un même opérateur hermitique
d'un même opérateur hermitique ![]() et associés à deux
valeurs propres
et associés à deux
valeurs propres
![]()
![]() sont
orthogonaux. En effet :
sont
orthogonaux. En effet :
Question 1-7 : Montrer que si un opérateur hermitique
![]() satisfait une équation algébrique
satisfait une équation algébrique
![]() R admet n valeurs propres distinctes et racines de l'équation
algébrique :
R admet n valeurs propres distinctes et racines de l'équation
algébrique :
![]() Tout ket
Tout ket ![]() est combinaison linéaire des
kets propres
est combinaison linéaire des
kets propres ![]() de R :
de R :
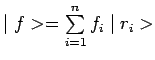
![]() Appliquez les résultats précédents aux cas
particuliers :
Appliquez les résultats précédents aux cas
particuliers : ![]() et
et
![]() .
.