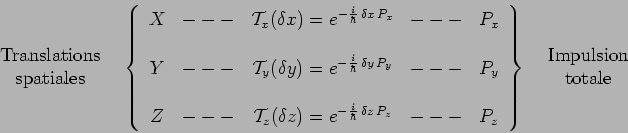Géométrie et dynamique

L'ensemble des principaux résultats obtenus dans ce chapitre peut être résumé dans les tableaux suivants, dans lesquels sont mis en vis-à-vis des transformations géométriques dans l'espace-temps physique et les observables dynamiques, qui sont génératrices de ces transformations :

$$\begin{array}{c} \mathrm{Translations} \\ \mathrm{spatiales}... ...rray}{c} \mathrm{Impulsion} \\ \mathrm{totale} \\ \end{array}$$

$$\begin{array}{c} \mathrm{Translations} \\ \mathrm{temporelle... ...{array}{c} \mathrm{Energie} \\ \mathrm{totale} \\ \end{array}$$

$$\begin{array}{c} \mathrm{Rotations} \\ \mathrm{spatiales} \\... ...ment} \\ \mathrm{angulaire} \\ \mathrm{total} \\ \end{array}$$

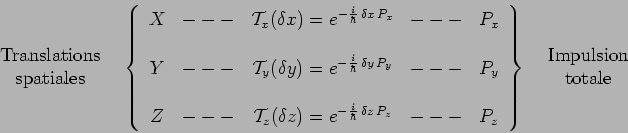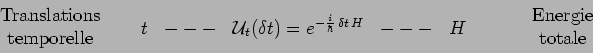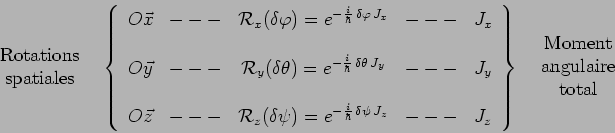Parce que le groupe des translations spatiales est commutatif, les composantes de l'impulsion totale commutent^IV10 :

$$\left[\mathcal{T}_x(\delta x),\mathcal{T}_y(\delta y)\right]=0 ~~~~\longleftrightarrow~~~~~\left[P_x,P_y\right]=0$$

Parce que le groupe des rotations n'est pas commutatif, les composantes du moment angulaire total ne commutent pas, et les propriétés de composition des rotations déterminent ces relations de commutation. En particulier parce que^IV11 :

$$\mathcal{R}_x(\delta).\mathcal{R}_y(\varepsilon).\mathcal{R}_z(-\delta). \mathcal{R}_y(-\varepsilon) = \mathcal{R}_z(\delta\varepsilon)$$

alors :

$$\left[J_x,J_y\right]=i\hbar\,J_z$$

Enfin, si le système étudié est isolé dans l'espace au cours de l'évolution temporelle considérée, et si :

$$H~\not=~H(t)$$

alors :

$$\left. \begin{array}{ccc} \left[P_x,H\right]=0 & ~~~~~~~~~ & ... ...d{array}\right\}~~~~\mathrm{Conservation~de~l'impulsion~totale}$$

$$\left. \begin{array}{ccc} \left[J_x,H\right]=0 & ~~~~~~~~~ & ... ...ray}\right\}~~~~\mathrm{Conservation~du~moment~angulaire~total}$$

$$\left. \begin{array}{ccc} \left[H,H\right]=0 & ~~~~~~~~~ & H=... ...y}\right\}~~~~\mathrm{Conservation~de~l'\acute{e}nergie~totale}$$

Les correspondances qui viennent ainsi d'être mises en évidence sont les premières manifestations d'une géométrisation possible de la physique. La physique est essentiellement une étude des interactions, c'est-à-dire une dynamique. Or, la dynamique est toujours difficile et opaque (pensez aux notions de masse, de force...). La géométrie de l'espace-temps est plus claire. Il y a donc avantage à rattacher, et même à fonder la dynamique sur la géométrie.

Précédemment, nous n'avons considéré comme groupes de transformations de symétrie, que le groupe des translations et celui des rotations. Si on considère le groupe de Poincaré (translations et transformations de Lorentz), on fait naturellement apparaître les notions de spin et de masse, et donc leurs raisons d'être. D'autres symétries, dites internes, et plus cachées, sont à l'origine des théories modernes, dites de jauge, dont le développement actuel laisse espérer une sorte de géométrisation complète de la physique, grâce à laquelle toutes les interactions physiques pourraient être régies par une même théorie, dite unifiée.