Correspondance avec la mécanique classique

Soit un système physique classique dont les états sont répérés dans la mécanique classique par les valeurs prises à chaque instant $t$ par un ensemble de coordonnées généralisées $q_1,q_2,\ldots,q_i,\ldots$ et par les moments canoniquement conjugués $p_1,p_2,\ldots,p_i,\ldots$ . Les équations du mouvement peuvent s'écrire sous la forme de Hamilton :

$${{dq_i}\over{dt}}={{\partial\mathcal{H}}\over{\partial p_i}}~~~~~~~~~~~ {{dp_i}\over{dt}}=-{{\partial\mathcal{H}}\over{\partial q_i}}$$

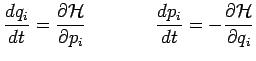$\mathcal{H}$ désignant la fonction, dite de Hamilton, et qui exprime l'énergie totale du système étudié en fonction des variables :

$$q_1,q_2,\ldots,q_i,\ldots,q_N~~~~~~\mathrm{et}~~~~~~ p_1,p_2,\ldots,p_i,\ldots,p_N$$

et éventuellement du temps :

$$\mathcal{H}=\mathcal{H}(q_i,p_j,t)~~~~~~~(i,j=1,2,\ldots,N)$$

et $N$ désignant le nombre de degrés de liberté du système.

On sait que toute variable dynamique $\hat{A}$ de ce système est , à l'instar de $\mathcal{H}$ , une fonction des mêmes variables :

$$\hat{A}=\hat{A}(q_i,p_j,t)$$

On en déduit alors :

$$\frac{d\hat{A}}{dt}=\sum\limits_{i=1}^N\,\left(\frac{\partial\hat... ...at{A}}{\partial p_i}\,\frac{dp_i}{dt}\right)+\frac{\partial\hat{A}}{\partial t}$$

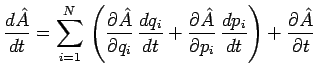ou encore, tenu compte des équations de Hamilton :

$$\frac{d\hat{A}}{dt}=\sum\limits_{i=1}^N\,\left(\frac{\partial\hat... ...ac{\partial\mathcal{H}}{\partial q_i}\right)+\frac{\partial\hat{A}}{\partial t}$$

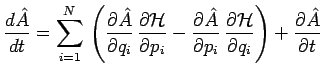et en introduisant le crochet de Poisson classique de $\hat{A}$ et $\mathcal{H}$ :

$$\frac{d\hat{A}}{dt}=\left(\hat{A},\mathcal{H}\right)+\frac{\partial\hat{A}}{\partial t}$$

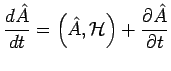Si, conformément à la méthode de quantification de Dirac, on remplace les grandeurs classiques $\hat{A}$ et $\mathcal{H}$ par les observables images $A_H$ et $H_H$ écrites dans le mode de représentation de Heisenberg, et le crochet de Poisson classique par le crochet de Poisson quantique et ce dernier par le commutateur correspondant, on obtient alors :

$$\left(\hat{A},\mathcal{H}\right)~~\longrightarrow~~ \left<A_H,H_H\right>=(i\hbar)^{-1}\left[A_H,H_H\right]$$

on obtient bien les équations de Heisenberg qui régissent l'évolution des observables :

$$i\hbar\,\frac{d}{dt}A_H=\left[A_H,H_H\right]+i\hbar\,\frac{\partial\hat{A}}{\partial t}$$