Dans le mode de représentation de Heisenberg les constantes du mouvement sont
particulièrement manifestes. En effet, si la grandeur classique ![]() ne
dépend pas du temps son image quantique dans le mode de représentation de
Schrödinger
ne
dépend pas du temps son image quantique dans le mode de représentation de
Schrödinger ![]() n'en dépend pas non plus et le dernier terme est nul. Si de
plus
n'en dépend pas non plus et le dernier terme est nul. Si de
plus ![]() commute avec l'hamiltonien :
commute avec l'hamiltonien :
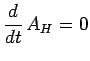 |
Dès lors l'observable ![]() admet une représentation mathématique
constante et ses vecteurs propres sont eux-mêmes constants. C'est en
particulier le cas du hamiltonien quand la fonction de Hamilton
admet une représentation mathématique
constante et ses vecteurs propres sont eux-mêmes constants. C'est en
particulier le cas du hamiltonien quand la fonction de Hamilton
![]() ne
dépend pas du temps. Les vecteurs propres sont alors les états stationnaires
déjà considérés précédemment dans le mode de représentation de
Schrödinger.
ne
dépend pas du temps. Les vecteurs propres sont alors les états stationnaires
déjà considérés précédemment dans le mode de représentation de
Schrödinger.