Toute évolution temporelle d'un système n'a de réalité que si
cette évolution est observée expérimentalement. Celle-ci est
alors réductible à une suite d'événements observables,
dont chacun est une mesure, et cette suite d'événements
constitue l'inventaire d'une histoire de ce système. Par
exemple, quand une particule chargée traverse une chambre à
bulles, elle laisse derrière elle, le long de son passage, un
chapelet de bulles. Chacune de ces bulles localise partiellement
la particule, en localisant l'événement où celle-ci a
interagi avec le liquide de la chambre. Cet événement a une
date ![]() et constitue ici une mesure des observables de position
et constitue ici une mesure des observables de position
![]() . Pour adopter une notation plus générale, ces
observables seront désignées globalement
. Pour adopter une notation plus générale, ces
observables seront désignées globalement ![]() . Le volume de la
bulle définit ici le domaine
. Le volume de la
bulle définit ici le domaine
![]() des valeurs propres de
des valeurs propres de
![]() non exclues. A cette mesure, le formalisme associe le
projecteur
non exclues. A cette mesure, le formalisme associe le
projecteur
![]() :
:
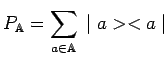 |
la somme portant sur tous les vecteurs d'une base du sous-espace
associé aux valeurs
![]() .
.
Considérons donc à présent une suite de tels événements apparus aux instants
successifs
![]() etc, et adoptons la représentation de
Heisenberg de telle sorte qu'entre deux mesures consécutives le vecteur
d'état demeure constant. Par contre, les observables mesurées sont fonction
du temps :
etc, et adoptons la représentation de
Heisenberg de telle sorte qu'entre deux mesures consécutives le vecteur
d'état demeure constant. Par contre, les observables mesurées sont fonction
du temps :
Ces mesures successives peuvent en général concerner des observables
différentes notées
![]() etc. De toute manière, à chacune de
ces mesures sera associé un projecteur qui, dans la représentation de
Heisenberg a pour expression simplifiée :
etc. De toute manière, à chacune de
ces mesures sera associé un projecteur qui, dans la représentation de
Heisenberg a pour expression simplifiée :
avec :
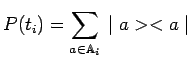 |
en notant ![]() l'instant où la mesure de
l'instant où la mesure de ![]() a été
effectuée. L'histoire des événements successifs considérés ci-dessus
peut donc être définie par le symbole simple
a été
effectuée. L'histoire des événements successifs considérés ci-dessus
peut donc être définie par le symbole simple
![]() et nous nous proposons de déterminer la
probabilité de réalisation d'une telle histoire.
et nous nous proposons de déterminer la
probabilité de réalisation d'une telle histoire.
Si ![]() =
=
![]() représente l'état initial du système et
représente l'état initial du système et
![]() le ket état normalisé consécutif à la
mesure effectuée à l'instant
le ket état normalisé consécutif à la
mesure effectuée à l'instant ![]() , nous obtenons
successivement :
, nous obtenons
successivement :
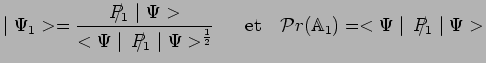 |
et de même pour la deuxième mesure :
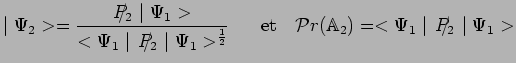 |
d'où :
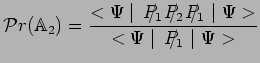 |
et donc pour deux mesures consécutives :
ou encore en injectant l'opérateur unité :
ou encore plus généralement, si l'état initial est un mélange
caractérisé par son opérateur densité :
Ces dernières expressions se généralisent immédiatement au cas d'un nombre quelconque de mesures successives et affectent chacune de ces histoires possibles de sa probabilité de réalisation. Notons toutefois que chacune des mesures intermédiaires ne peut porter que sur un ensemble de mesures compatibles, c'est-à-dire un ensemble d'observables qui commutent.