Mode de représentation ``interaction''

Il est encore possible de choisir un autre mode de représentation $\mathcal{R}(I)$ intermédiaire entre les deux modes précédents $\mathcal{R}(S)$ et $\mathcal{R}(H)$ . Un tel choix se révèle particulièrement utile quand le hamiltonien peut s'écrire sous la forme d'une somme de deux termes :

$$H=H^0+V$$

telle que le premier $H^0$ décrit la principale composante de l'énergie du système, elle-même constituée des énergies associées à ses constituants approximativement indépendants et telle que le second $V$ décrit les interactions supposées plus faible entre ces constituants. A partir du mode de représentation de Schrödinger, on effectue alors la transformation unitaire suivante, définie au moyen de l'opérateur d'évolution associé au terme principal $H^0$ du hamiltonien complet $H$ :

$$\mathcal{U}_0(t,t_0)=e^{-\frac{i}{\hbar}(t-t_0)\,H^0}$$

$$\begin{array}{ccc} \mid K>_S & ~~~\longrightarrow~~~ & \mid K... ...w~~~ & A_I = \mathcal{U}_0^{-1}\,A_S\,\mathcal{U}_0 \end{array}$$

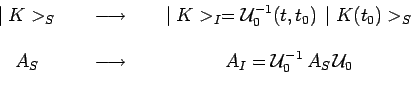Un calcul semblable à celui déjà effectué précédemment permet d'établir les équations d'évolution temporelle des vecteurs kets et des observables définis dans la représentation $\mathcal{R}(I)$ :

$$i\hbar\,\frac{d}{dt}\mid K(t)>_I = V_I \mid K(t)>_I$$

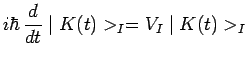$$i\hbar\,\frac{d}{dt}A_I(t) = \left[A_I,H_I^0\right]+ i\hbar\,\frac{\partial}{\partial t} A_I$$