Invariance galiléenne de l'équation de Schrödinger

Il s'agit de démontrer qu'un changement de référentiel galiléen est une transformation inobservable pour des observateurs liés à ces référentiels. A cet effet, il faut montrer que l'équation de Schrödinger est invariante dans les transformations de Galilée.

La transformation de Galilée est dite active quand elle change les états physiques et les observables. Son expression mathématique a déjà été déterminée^IV13 :

$$G(\vec{V},t) = e^{\frac{i}{\hbar}\,\vec{V}\,(M\, \vec{R} - t\,\vec{P})}$$

Il faut alors montrer que si $\mid K(t)>$ désigne un état d'évolution possible du système physique $S$ , le nouvel état :

$$\mid K^\prime(t)> = G(\vec{V},t)\,\mid K(t)>$$

désigne un autre état d'évolution également possible du système $S$ . Bref, il faut montrer que si $\mid K(t)>$ satisfait l'équation de Schrödinger, l'état $\mid K^\prime(t)>$ la satisfait également.

Supposons donc :

$$i\hbar\,\frac{d}{dt}\,\mid K(t)> = H\,\mid K(t)>$$

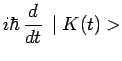d'où il résulte, en multipliant les deux membres par l'opérateur $G(\vec{V},t)$ :

$$i\hbar\,G\left(\frac{d}{dt}\,\mid K(t)>\right) = i\hbar\,\frac{d}{dt}\,G\mid K(t)> - \left( i\hbar\,\frac{dG}{dt}\right)\,\mid K(t)> ~=~ G\,H\,\mid K(t)>$$

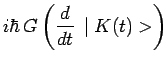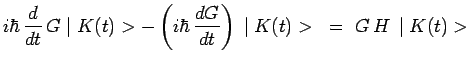Tenu compte de l'identité :

$$e^{A+B} = e^A\,\cdot\,e^B\,\cdot\,e^{-\frac{1}{2}[A,B]}$$

et en choisissant l'axe $O\vec{x}$ orienté par la vitesse $\vec{V}$ :

$$G(\vec{V},t) = e^{\frac{i}{\hbar}\,V\,(M\,X - t\,P_x)} ~=~ e^{-\frac{i}{\hbar}\,... ...x}\,~e^{\frac{i}{\hbar}\,M\,V\,X}\,~e^{\frac{i}{\hbar}\,\frac{1}{2}\,M\,V^2\,t}$$

$$i\hbar\,\frac{dG}{dt} = \left( V\,P_x - \frac{1}{2}\,MV^2 \right)\,G$$

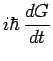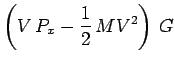et puisque par ailleurs^IV14 :

$$H^\prime ~=~ G\,H\,G^{-1} = H - V\,P_x + \frac{1}{2}\,MV^2$$

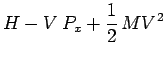l'équation précédente conduit au résultat annoncé :

$$i\hbar\,\frac{d}{dt}\,G\mid K(t)> = H\,G\,\mid K(t)>$$

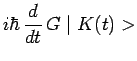soit :

$$i\hbar\,\frac{d}{dt}\,\mid K^\prime(t)> = H\,\mid K^\prime(t)>$$

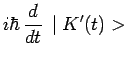Par ailleurs, la transformation de Galilée est dite passive quand elle laisse les états physiques et les observables invariants. Elle correspond alors seulement à un changement de référentiel. Il faut alors montrer que la fonction d'onde de l'état $\mid K>$ dans le référentiel $\Sigma$ , satisfait la même équation mathématique que la fonction d'onde $K^\prime$ représentative du même état $\mid K>$ dans le référentiel $\Sigma^\prime$ . Bref, il faut montrer que l'équation de Schrödinger est invariante dans un référentiel galiléen^IV15 :

$$i\hbar\,\frac{d}{dt}\,K^\prime(t) = H^\prime\,K^\prime(t) ~~~~~~~~~~~\longleftrightarrow~~~~~~~~~~~ i\hbar\,\frac{d}{dt}\,K(t) ~=~ H\,K(t)$$

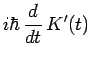A cet effet, il y a lieu de remarquer que changer de référentiel $\Sigma~\to~\Sigma^\prime$ c'est changer les vecteurs de base $\mid x,y,z>$ de la représentaion de Schrödinger :

Quand $\Sigma~~\longrightarrow~~\Sigma^\prime~~~~~~~~~~~~~~~~~~~~~~~~~~\mid x,\ldots>~~\longrightarrow~~\mid x,\ldots>^\prime$

de telle sorte que :

$$G\,\mid x^\prime,\ldots > ~=~ \mid x^\prime,\ldots >^\prime = e^{-\frac{i}{\hbar}\,\frac{M\,V^2}{2}\,t}\,~e^{\frac{i}{\hbar}\,M\,V\,X}\,~e^{-\frac{i}{\hbar}\,V\,t\,P_x} \,\mid x^\prime,\ldots >$$

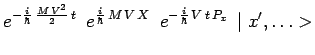et en remarquant la présence de l'opérateur de déplacement, avec $\mid x^\prime + V\,t>~=~\mid x>$ , on obtient :

$$\mid x^\prime,\ldots >^\prime = e^{\frac{i}{\hbar}\,\left(M\,V\,X - \frac{1}{2}\,M\,V^2\,t\right)}\,\mid x,\ldots >$$

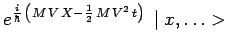et en rappelant la définition des fonctions d'onde dans $\Sigma$ et dans $\Sigma^\prime$ :

$$< x, \ldots \mid K(t) > = K(x,\ldots,t)~~~~~~~~~~~~~~~~~~~~~~~~ {~}^\prime<x^\prime,\ldots \mid K(t) > ~=~ K^\prime(x^\prime,\ldots, t)$$

la loi de transformation de la fonction d'onde :

$$\begin{array}{ccl} K^\prime(x^\prime,\ldots,t) &=& e^{-\frac{... ... & \\ & = & e^{-i\,\alpha(x,t)}\,K(x,\ldots,t) \\ \end{array}$$

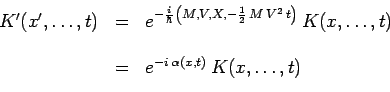On notera que les variables $x$ et $x^\prime$ désignent ci-dessus et exclusivement les abscisses du centre de masse, les variables relatives internes étant laissées invariantes.

Supposons que dans $\Sigma^\prime$ la fonction d'onde $K^\prime(x^\prime,\ldots,t)$ du système physique satisfasse l'équation de Schrödinger :

$$i\hbar\,\frac{\partial}{\partial t^\prime}\,K^\prime(x^\prime,\ldots,t) = H^\prime\,K^\prime(x^\prime,\ldots,t)~~~~~~~~~~~~~~\mathrm{avec}~... ...frac{-\hbar^2}{2M}\,\frac{\partial^2}{\partial x^{\prime\,2}}\,+\,\Omega^\prime$$

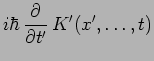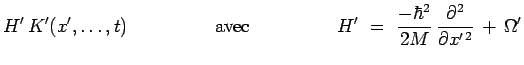$\Omega^\prime$ désignant une fonction des seules variables internes.

Il faut, dans l'équation précédente, effectuer le changement de fonction :

$$K^\prime(x^\prime,\ldots,t) = e^{-i\,\alpha(x,t)}\,K(x,\ldots,t)$$

et le changement de variable :

$$x^\prime = x - V\,t~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~t^\prime~=~t$$

On obtient alors successivement :

$$\mathrm{avec}~~~~~~~~~~~~\frac{\partial}{\partial t^\prime}~=~\fr... ...~~~~~~~~~~~~~~~\frac{\partial}{\partial x^\prime}~=~\frac{\partial}{\partial x}$$

$$i\hbar\,\frac{\partial\,K^\prime}{\partial t^\prime} = e^{-i\,\alpha}\,\left( -\frac{1}{2}\,M\,V^2 + i\hbar\,\frac{\partial}{\partial t} + M\,V^2 + i\hbar\,V\,\frac{\partial}{\partial x}\right)\,K$$

$$\begin{array}{ccl} H^\prime\,K^\prime &=& \left( \scalebox{1.... ...1}{2}$}\,M\,V^2 - V\,P_x + P_x^2 + \Omega\right)\,K \end{array}$$

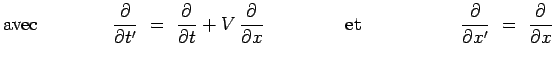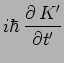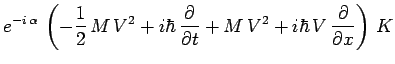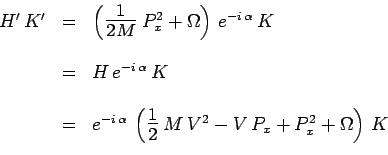d'où résulte finalement :

$$i\hbar\,\frac{\partial}{\partial t}\,K(x,\ldots,t) = H\,K(x,\ldots,t)$$

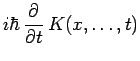L'équation de Schrödinger est donc bien invariante dans un changement de référentiel galiléen.