Considérons dans un espace à une dimension ![]() l'état
initial
l'état
initial ![]() d'une particule telle que :
d'une particule telle que :
Le produit initial des dispersions inévitables
![]() sur
sur
![]() et
et
![]() sur
sur ![]() prend sa valeur minimum pour des
fonctions d'onde gaussiennes :
prend sa valeur minimum pour des
fonctions d'onde gaussiennes :
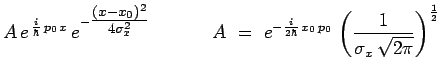 |
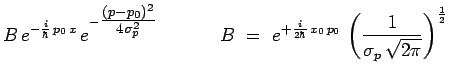 |
transformées de Fourier l'une de l'autre et telles que
:
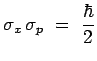 |
L'évolution temporelle d'un tel état s'en déduit par
application de l'opérateur d'évolution :
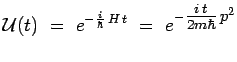 |
si la particule ne subit aucune interaction :
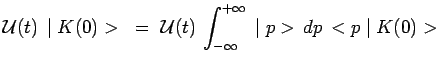 |
et puisque ![]() est vecteur propre de
est vecteur propre de ![]() avec la
valeur propre :
avec la
valeur propre :
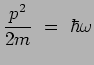 |
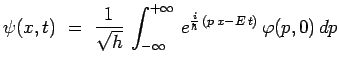 |
qui peut encore s'écrire, avec
![]() et
et
![]() :
:
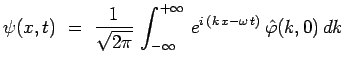 |
où :
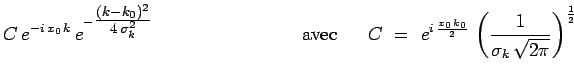 |
![]() est une fonction de
est une fonction de ![]() , qui définit la loi de
dispersion des ondes et qui peut être développée dans le
voisinage
, qui définit la loi de
dispersion des ondes et qui peut être développée dans le
voisinage ![]() de la valeur principale
de la valeur principale ![]() qui donne
à
qui donne
à
![]() sa valeur maximale :
sa valeur maximale :
avec :
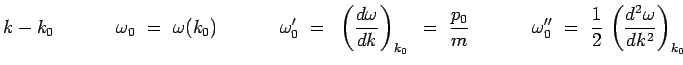 |
En reportant ce développement limité de ![]() dans
l'intégrale, et en posant :
dans
l'intégrale, et en posant :
on obtient une expression :
![$\displaystyle \frac{C}{\sqrt{2\pi}}\,e^{i\,[k_0\,(x-x_0)-\omega_0\,t]}\,
\int^{...
...fty}_{-\infty}\,e^{i\,\bar{k}\,\bar{x}}\,e^{-\bar{\alpha}\,\bar{k}^2}\,d\bar{k}$](img3066.png) |
Sur cette expression, on remarque que le centre du paquet d'ondes
![]() (où la phase est stationnaire) :
(où la phase est stationnaire) :
| 0 | 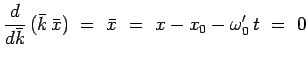 |
se déplace avec la vitesse de groupe égale à
![]() qui correspond à la
vitesse classique
qui correspond à la
vitesse classique ![]() de la particule. Par ailleurs on
remarque sur l'expression de
de la particule. Par ailleurs on
remarque sur l'expression de
![]() :
:
On en déduit que la dispersion de l'impulsion ![]() autour de sa
valeur moyenne constante
autour de sa
valeur moyenne constante ![]() est elle-même constante et
toujours égale à sa valeur initiale
est elle-même constante et
toujours égale à sa valeur initiale ![]() . Cette
constance résulte du fait que pour le hamiltonien d'une
particule libre, l'impulsion est une constante du mouvement.
. Cette
constance résulte du fait que pour le hamiltonien d'une
particule libre, l'impulsion est une constante du mouvement.
Après intégration, la fonction d'onde s'écrit encore :
 |
de telle sorte que la distribution de localisation
possible de la particule :
![$\displaystyle R\,\exp\left(-\frac{(x-x_0-\omega_0^\prime\,t)^2}{2\,(\sigma_x^2 ...
...
+
\frac{\omega_0^{\prime\prime}\,t^2}{\sigma_x^2}\right)\right]^{-\frac{1}{2}}$](img3077.png) |
se déplace bien avec la vitesse
![]() et avec une dispersion :
et avec une dispersion :
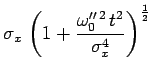 |
qui augmente indéfiniment au cours du temps et devient infiniment grande.