|
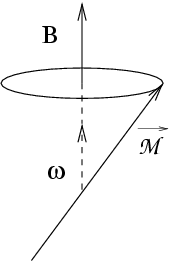
Quand un système physique, un atome par exemple, doté d'un moment
angulaire total 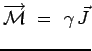 est plongé dans
un champ magnétique extérieur uniforme
est plongé dans
un champ magnétique extérieur uniforme
|
|
|
L'étude de ce phénomène présente un double
intérêt. D'une part elle constitue une application directe du
formalisme quantique, d'autre part elle indique pourquoi et
comment la physique classique peut représenter par des vecteurs des
grandeurs physiques telles que ![]() et
et
![]() qui en fait doivent être
représentées par des opérateurs quantiques.
qui en fait doivent être
représentées par des opérateurs quantiques.
L'explication quantique du phénomène est immédiate. En
effet, l'expression classique de l'énergie d'interaction fournit
l'expression quantique du hamiltonien dans l'espace des états de
spin de l'atome :
en choisissant la direction de ![]() pour celle de
l'axe
pour celle de
l'axe ![]() . L'opérateur d'évolution temporelle :
. L'opérateur d'évolution temporelle :
peut être considéré comme un opérateur de
rotation autour de l'axe ![]() , puisque
, puisque ![]() désigne la
composante selon cet axe du moment angulaire total de l'atome dans
son référentiel propre :
désigne la
composante selon cet axe du moment angulaire total de l'atome dans
son référentiel propre :
Il en résulte bien que l'état de spin du système et donc son
orientation dans l'espace, tourne autour de la direction de
![]() :
:
avec la vitesse angulaire :
La transposition classique de cette étude quantique consiste à considérer un grand nombre de systèmes identiques et à utiliser les équations de Ehrenfest et donc à n'examiner que l'évolution temporelle des valeurs moyennes.
A chaque instant ![]() , quand le système est dans l'état
, quand le système est dans l'état ![]() , on
définit par ses composantes le vecteur classique :
, on
définit par ses composantes le vecteur classique :
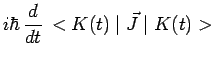 |
![$\displaystyle <K\mid
\left[\vec{J},H\right]\mid K>$](img3114.png) |
Si ![]() désigne le hamiltonien dans le référentiel propre
et en absence de champ :
désigne le hamiltonien dans le référentiel propre
et en absence de champ :
Si seul ![]() oriente l'espace, celui-ci est isotrope en
absence de champ et :
oriente l'espace, celui-ci est isotrope en
absence de champ et :
![$\displaystyle \left[\vec{J},H_0\right]$](img3116.png) |
0 |
de telle sorte que, par exemple pour la composante ![]() :
:
![\begin{displaymath}\begin{array}{ccl}
\left[J_x,H\right] &=& -\gamma\,\left[J_x,...
...,g\,\gamma\,\left(\vec{B}\wedge\vec{J}\right)_x \\
\end{array}\end{displaymath}](img3117.png) |
et plus généralement :
![$\displaystyle \left[\vec{J},H\right]$](img3118.png) |
de telle sorte que les équations de Ehrenfest
s'écrivent :
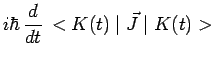 |
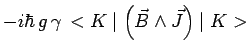 |
ou encore, en introduisant le vecteur classique moment
angulaire
![]() :
:
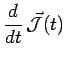 |
De cette équation classique on déduit immédiatement :
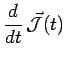 |
|
|