Tout état physique, notamment l'état d'une particule, est
soumis à l'action de l'opérateur évolution temporelle
![]() :
:
qui s'écrit dans la représentation de Schrödinger :
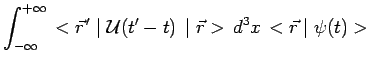 |
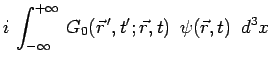 |
en introduisant la fonction de Green ![]() encore
appelée propagateur, définie par :
encore
appelée propagateur, définie par :
![]() désignant le hamiltonien supposé indépendant
du temps.
désignant le hamiltonien supposé indépendant
du temps.
Cette fonction de Green peut être considérée comme étant
l'amplitude de probabilité de localiser la particule au point
![]() à l'instant
à l'instant ![]() , sachant que cette
particule était localisée au point
, sachant que cette
particule était localisée au point ![]() à l'instant
à l'instant
![]() . Puisque ces états localisés ne sont pas normalisables, la
fonction de Green est une fonction singulière. Son expression
peut néanmoins être calculée en procédant comme suit :
. Puisque ces états localisés ne sont pas normalisables, la
fonction de Green est une fonction singulière. Son expression
peut néanmoins être calculée en procédant comme suit :
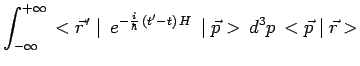 |
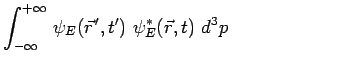 |
avec :
 |
ou encore très explicitement :
![$\displaystyle h^{-3}\,\int^{+\infty}_{-\infty}\,\exp\,\frac{i}{\hbar}\,\left[\,...
...c{r}^{\,\prime}-\vec{r})
- \frac{\vec{p}^{\,2}}{2m}\,(t^\prime-t)\,\right]~d^3p$](img3146.png) |
Pour calculer l'intégrale, on introduit la variable :
 |
et tenu compte du résultat :
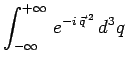 |
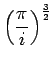 |
on obtient l'expression finale du propagateur non
relativiste :
![\begin{displaymath}\begin{array}{\vert c\vert}\hline { }\\ ~~i\,G_0(\vec{r}^{\,\...
...{r}^{\,\prime}-\vec{r})^2\,\right]~~\\ { }\\ \hline \end{array}\end{displaymath}](img3151.png) |
La théorie du mouvement brownien démontre que la
probabilité pour une particule soumise à des chocs
aléatoires, de passer de la position ![]() à l'instant
à l'instant
![]() , à une position
, à une position
![]() à l'instant
à l'instant
![]() où
où
![]() a une expression toute semblable
qui s'obtient en remplaçant
a une expression toute semblable
qui s'obtient en remplaçant
![]() par
par ![]() dans
l'expression de
dans
l'expression de ![]() .
.