Ensemble Complet d'Observables qui Commutent (ou ECOC)

Soit $A$ une observable et supposons qu'aucune de ses valeurs propres n'est dégénérée. Tout ket $\mid f>$ peut alors être décomposé comme suit :

$\mid f>=\sum\limits_i~f_i~\mid a_i>~~~~~$ (spectre discret)

$\mid f>=\int_\Delta f(a)\mid a>da~~~~~$ (spectre continu)

$\mid f>=\sum\limits_i f_i\mid a_i>+\int_\Delta f(a)\mid a>da~~~$ (spectre mixte)

Question 1-12 : Démontrez que la décomposition spectrale précédente du ket $\mid f>$ est bien unique.

Nous adopterons dans tous les cas, la notation symbolique suivante :

$\mid f>=\underset{a\in\Delta}{\scalebox{2.0}{S}}~ f(a)\mid a>~~~~~$

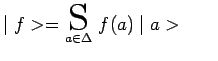
S désignant une somme $\sum$ ou une intégrale $\int$ selon que la variable $a$ sur laquelle on effectue la somme est discrète ou continue, et $\Delta$ désignant l'ensemble des valeurs propres de $A$ .

Si les valeurs propres $a$ sont dégénérées, il faut, pour obtenir un système complet, introduire dans la somme S une base complète $\mid a,x>,~x\in\Delta(a)$ , dans chacun des sous-espaces $\cal{H}_{\cal{S}}$ ($a$ ) associés à chacune des valeurs propres $a$ dégénérée :

$\mid f>=\underset{a,x}{\scalebox{2.0}{S}}~ f(a,x)\mid a,x>~~~~~a\in\Delta~~~~x\in\Delta(a)$

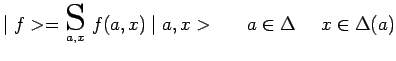
La base complète ${\mid a,x>}$ considérée ci-dessus, n'est pas bien définie puisque dans chacun des sous-espaces $\cal{H}_{\cal{S}}$ ($a$ ), il existe une infinité de manières distinctes de choisir une base partielle.

Comment construire une base bien déterminée ? A cet effet, nous allons démontrer qu'il est toujours possible de construire un ensemble d'observables $A,B,\ldots,Z$ qui commutent deux à deux et qui admettent un ensemble complet et unique d'états propres communs $\mid a,b,\ldots,z>$ tels que pour tout vecteur ket $\mid f>$ on ait :

$\mid f>=\underset{a,b,\ldots,z}{\scalebox{2.0}{S}}~f(a,b,\ldots,z)\mid a,b,\ldots,z>$
$A\mid a,b,\ldots,z>=a\mid a,b,\ldots,z>,\ldots , Z\mid a,b,\ldots,z>=z\mid a,b,\ldots,z>$

A tout ensemble de valeurs propres simultanées $a,b,c,\ldots,z$ ne correspond alors qu'un seul état propre commun noté $\mid a,b,c,\ldots,z>$ . Le système complet ${\mid a,b,c,\ldots,z>}$ est alors unique.