f) Projecteur

suivant: Ensemble Complet d'Observables qui monter: Valeurs et vecteurs propres précédent: e) Observable Table des matières

f) Projecteur

$\mid f>$ et $\mid g>$ désignant deux vecteurs kets quelconques non nuls, on définit dans $\cal{H}_{\cal{S}}$ l'opérateur $P_{fg}$ tel que :

$\forall \mid h>~\in~$ $\cal{H}_{\cal{S}}$ $~~~~~~~~~~~~~~~~~~~~~~~~~~~P_{fg}\mid h>=\mid f><g\mid h>$

$\imath-$ $P_{fg}$ est un opérateur linéaire dans $\cal{H}_{\cal{S}}$ puisque le vecteur bra $<g\mid$ désigne une forme linéaire

$P_{fg}(\lambda_1\mid h_1>+\lambda_2\mid h_2>) =\mid f><g\mid (\lambda_1\mid h_1>+\lambda_2\mid h_2>)$

$=\lambda_1\mid f><g\mid h_1>+\lambda_2\mid f><g\mid h_2>$

$=\lambda_1 P_{fg}\mid h_1>+\lambda_2P_{fg}\mid h_2>$

$\imath\imath-$ L'action de $P_{fg}$ dans $\cal{H}_{\cal{S}}^*$ s'en déduit :

$(<u\mid P_{fg})\mid h>=<u\mid (P_{fg}\mid h>)=<u\mid (\mid f><g\mid h>)$

$<u\mid f><g\mid h>=(<u\mid f><g\mid )\mid h>$

et donc $<u\mid P_{fg}=<u\mid f><g\mid$

$P_{fg}$ est donc un opérateur linéaire qui dans $\cal{H}_{\cal{S}}$ projette sur la direction du ket $\mid f>$ , et qui dans $\cal{H}_{\cal{S}}^*$ projette sur la direction du bra $<g\mid$ .

Des deux relations de définition :

$P_{fg}\mid h>=\mid f><g\mid h>~~~$ et $~~~<u\mid P_{fg}=<u\mid f><g\mid$

il résulte qu'il est d'écrire l'opérateur $P_{fg}$ sous la forme :

$P_{fg}=\mid f><g\mid$

et cette nouvelle notation est seulement une convention d'écriture.

$\imath\imath\imath-$ L'opérateur adjoint $P_{fg}^\dagger$ de $P_{fg}$ définit le bra conjugué de $P_{fg}\mid h>$ :

$P_{fg}\mid h>~~\longleftrightarrow~~<h\mid P_{fg}^\dagger$

$\mid f><g\mid h>~~\longleftrightarrow~~<h\mid g>\mid f>=<h\mid (\mid g>\mid f>)$

d'où il résulte immédiatement que :

$P_{fg}^\dagger= \mid g><f\mid$

Question 1-10 : Quels sont les vecteurs propres et les valeurs propres de $P_{fg}$ ?

Dans la suite, on considèrera le plus souvent des opérateurs de projection de la forme :

$P= \mid f><f\mid$ , avec $~~<f\mid f>=1$

dotés des deux propriétés typiques :

$P= P^\dagger$ et

Plus généralement, considérons une suite de vecteurs orthonormés ${\mid i>}$ où $i=1,2,\ldots,n$ . Ces vecteurs constituent une base orthonormée d'un sous-espace ${\cal{E}}_n\in{\cal{H}}$ à dimensions et permettent de construire un opérateur somme de projecteurs :

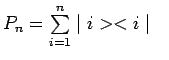$P_n= \sum\limits_{i=1}^{n}\mid i><i\mid ~~$ avec $~~<i\mid j>=\delta_{ij}$

qui est lui-même un projecteur dans ${\cal{E}}_n$ :

$P_n^\dagger=P_n~~$ et

$\forall f~\in~{\cal{H}}~~~~~~~~~~~~~~~~~~~~~~~~~~~P_n\mid f>~\in~{\cal{E}}_n$

Question 1-11 : Démontrez que tout opérateur hermitique P satisfaisant l'équation est un projecteur dans le sous-espace associé à sa valeur propre égale à 1.

suivant: Ensemble Complet d'Observables qui monter: Valeurs et vecteurs propres précédent: e) Observable Table des matières

Arnaud Balandras 2005-04-02