Considérons une particule de spin ![]() . Nous savons
déjàV1 que l'espace de ses états
. Nous savons
déjàV1 que l'espace de ses états
![]() est le produit d'un premier espace mathématique de
Hilbert
est le produit d'un premier espace mathématique de
Hilbert
![]() dit de configuration, associé aux
états localisés ou d'impulsion de cette particule, dans
l'espace physique à trois dimensions, et d'un deuxième espace
mathématique
dit de configuration, associé aux
états localisés ou d'impulsion de cette particule, dans
l'espace physique à trois dimensions, et d'un deuxième espace
mathématique
![]() à
à ![]() dimensions associé aux
états de spin de cette particule, et donc à son orientation
dans le même espace physique.
dimensions associé aux
états de spin de cette particule, et donc à son orientation
dans le même espace physique.
Ici encore, l'ensemble des deux E.C.O.C., l'un dans
![]() , l'autre dans
, l'autre dans
![]() , constitue un E.C.O.C. dans
, constitue un E.C.O.C. dans
![]() :
:
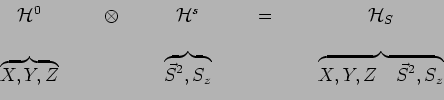 |
et un état de la particule pourra être représenté par un
vecteur ket tel que :
ou encore, en choisissant dans
![]() la représentation
de Schrödinger :
la représentation
de Schrödinger :
Mais un état quelconque n'est pas nécessairement factorisable,
et, par exemple pour une particule de spin
![]() V2 :
V2 :
Ici encore, une application directe du principe de Born dit que la probabilité
de localiser la particule dans un élément de volume ![]() centré sur un
point
centré sur un
point ![]() , et de mesurer en même temps (
, et de mesurer en même temps (![]() et
et ![]() sont compatibles)
sont compatibles)
![]() a pour expression :
a pour expression :
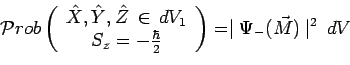 |