On notera soigneusement qu'une telle fonction d'onde dépendant
de six variables
![]()
![]() ne peut être
considérée comme définissant une onde classique se déplaçant dans l'espace physique à trois dimensions. La fonction d'onde,
comme le vecteur
ne peut être
considérée comme définissant une onde classique se déplaçant dans l'espace physique à trois dimensions. La fonction d'onde,
comme le vecteur ![]() qu'elle représente, est définie dans un
espace, non pas à six dimensions parce que six observables de
base, mais dont le nombre de dimensions est infini,
puisque cet espace est sous-tendu par les vecteurs
qu'elle représente, est définie dans un
espace, non pas à six dimensions parce que six observables de
base, mais dont le nombre de dimensions est infini,
puisque cet espace est sous-tendu par les vecteurs
![]() .
.
Par application du postulat de Born, connaître la fonction d'onde
![]() permet de répondre immédiatement à la question :
permet de répondre immédiatement à la question :
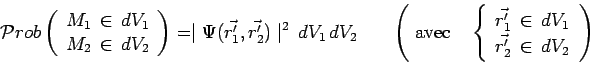 |
Si la fonction ![]() est factorisable :
est factorisable :
la probabilité précédente l'est également :
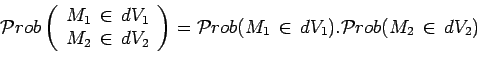 |
et les deux particules sont alors indépendantes.
En général la fonction
![]() n'est pas factorisable,
ce qui correspond au fait que le vecteur ket
n'est pas factorisable,
ce qui correspond au fait que le vecteur ket ![]() n'est pas lui-même un
produit tensoriel de type :
n'est pas lui-même un
produit tensoriel de type :
Les deux particules ne sont pas alors indépendantes, ce qui peut résulter de
leur interaction, par exemple électromagnétique. Précisément,
l'observable qui représente cette énergie potentielle d'interaction :
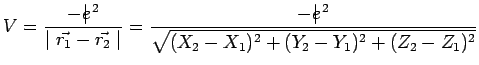 |
n'est évidemment pas décomposable en une somme et ses fonctions propres en un produit dans la représentation choisie.