Partition d'un système

Dans ce qui précède, l'espace complet des états est obtenu par produit tensoriel d'espaces associés à des parties du système complet. Inversement, un espace d'états peut parfois être factorisé en sous-espaces, dont chacun est associé à une partie des degrés de liberté du système.

Considérons, par exemple, l'espace $\mathcal{H}$ des états d'une particule de spin nul. Dans la représentation de Schrödinger, une base de cet espace est constituée des vecteurs propres :

$$\mid x,y,z>~~~~~~~~~~\mathrm{des~observables}~~~~~X,~Y,~Z$$

et $\mathcal{H}$ est engendré par combinaison linéaire de ces vecteurs de base.

On peut encore définir le sous-espace mathématique ${\mathcal{H}}_{x}$ engendré par les vecteurs propres de $X$ , considéré comme un E.C.O.C. à lui tout seul, et de même les sous-espaces ${\mathcal{H}}_{y}$ et ${\mathcal{H}}_{z}$ et on remarque :

$$\mathcal{H}= \mathcal{H}_x\otimes\,\mathcal{H}_y\otimes\,\mathcal{H}_z$$

Quand on considère une particule placée dans un espace à une dimension, c'est précisément dans l'un de ces sous-espaces que l'on suppose se placer.

On remarquera qu'ici encore, bien entendu, un vecteur ket de $\mathcal{H}$ n'est pas en général factorisable, ce qui est manifeste dans la représentation de Schrödinger :

$$\Psi(x,y,z)\not=f(x)\,g(y)\,h(z)$$

Dans une telle décomposition en facteurs, aucun des sous-espaces facteurs n'est associé à une partie du système complet. Chacun de ces sous-espaces est associé à l'une des observables d'un E.C.O.C., c'est-à-dire à l'un des degrés de liberté du système. A chaque E.C.O.C. choisi correspond une décomposition possible et, par suite, chacun des sous-espaces facteurs a seulement une signification opérationnelle, et ne correspond à aucune réalité physique indépendante.

La portée de cette remarque peut cependant déjà être étendue à des situations moins triviales. Par exemple, nous verrons dans l'étude de l'atome d'hydrogène, constitué d'un proton (masse $m_p$ , position $\vec{r_p}$ ) et d'un électron (masse $m_e$ , position $\vec{r_e}$ ) que ce système atomique est équivalent, du point de vue de son étude mathématique, à un système constitué de deux particules fictives appelées ``quasi-particules'', l'une $\Omega$ (masse $M$ , position $\vec{R}$ ) située au centre de masse, et l'autre $\omega$ (masse $m$ , position $\vec{r}$ ) avec :

$$\begin{array}{c} M_\Omega=m_p+m_e \\ { } \\ \frac{1}{m_\ome... ...\\ \vec{r}_\omega(x,y,z) = \vec{r_e}-\vec{r_p} \\ \end{array}$$

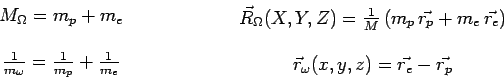Aux deux E.C.O.C. possibles correspondent deux factorisations de l'espace des états :

$$\vec{r_p}~~~~\mathrm{et}~~~~\vec{r_e}~~~~~~~~~~~~~~~~~~~~~~~~ \mathrm{ou}~~~~~~~~~~~~~~~~~~~~~~~~\vec{R}_\Omega~~~~\mathrm{et}~~~~ \vec{r}_\omega$$

$$\mathcal{H}_{{(x,y,z)}_p}\otimes\,\mathcal{H}_{{(x,y,z)}_e}=\mathcal{H}= \mathcal{H}_{{(X,Y,Z)}_\Omega}\otimes\,\mathcal{H}_{{(x,y,z)}_\omega}$$

Tandis que les deux particules ``réelles'' électron et proton, sont en interaction, et ne sont donc pas indépendantes, les deux quasi-particules $\Omega$ et $\omega$ sont indépendantes, et de ce fait constituent une meilleure décomposition du système total, et donc une meilleure partition.