En général, l'espace est isotrope pour le système étudié. Il en résulte
que son hamiltonien commute avec les opérateurs de rotation et donc avec les
composantes du moment total ![]() :
:
![$\displaystyle \left[H,\vec{J}\right]=0$](img3521.png) |
On est donc amené à rechercher les fonctions propres de ![]() parmi celle de
parmi celle de
![]() et
et ![]() . Pour une particule de spin nul (
. Pour une particule de spin nul (![]() ) :
) :
mais, en général ![]() ne se réduit pas à
ne se réduit pas à
![]() .
Déjà pour une particule de spin
.
Déjà pour une particule de spin ![]() :
:
et pour un système constitué de plusieurs particules de moments
angulaires ![]() :
:
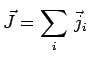 |
Dans le cas particulier de deux particules de moments angulaires ![]() et
et ![]() ,
on est donc amené à résoudre le problème suivant : connaissant les
valeurs propres et les fonctions propres des moments angulaires partiels
,
on est donc amené à résoudre le problème suivant : connaissant les
valeurs propres et les fonctions propres des moments angulaires partiels
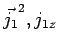 et
et
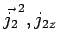 , en déduire les valeurs propres
et les fonctions propres de
, en déduire les valeurs propres
et les fonctions propres de ![]() et
et ![]() avec :
avec :
Les observables
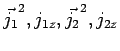 commutent deux à deux,
mais, en général, ne suffisent pas pour former un E.C.O.C. Pour cela il
faut leur ajouter d'autres observables qui seront notées ici globalement
commutent deux à deux,
mais, en général, ne suffisent pas pour former un E.C.O.C. Pour cela il
faut leur ajouter d'autres observables qui seront notées ici globalement ![]() .
Par ailleurs on remarque :
.
Par ailleurs on remarque :
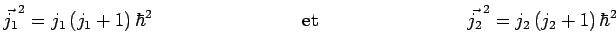 |