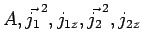 et supposés
déjà connus :
et supposés
déjà connus :
Soient
![]() les vecteurs propres communs
à
les vecteurs propres communs
à
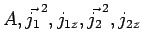 et supposés
déjà connus :
et supposés
déjà connus :
On remarque que ![]() et
et ![]() commutent avec
commutent avec
![]() et
et
![]() . Par suite les vecteurs propres de
. Par suite les vecteurs propres de ![]() et
et ![]() sont de la
forme :
sont de la
forme :
et peuvent être cherchés dans chacun des
sous-espaces
![]() sous-tendus par les
vecteurs
sous-tendus par les
vecteurs
![]() avec
avec
![]() bien
fixés et
bien
fixés et
![]() et
et
![]() .
.
Nous pouvons maintenant faire deux remarques importantes :
![]() A chaque valeur de
A chaque valeur de ![]() correspond une ou plusieurs
séries de
correspond une ou plusieurs
séries de ![]() vecteurs
vecteurs
![]() avec :
avec :
![]()
Cette seconde remarque nous montre que :
Nous connaissons donc toutes les valeurs propres ![]() de
de ![]() et leur ordre de
dégénérescence. Ces valeurs propres peuvent être classées par valeurs
décroissantes en indiquant sous chacune son ordre de dégénérescence.
Soit, par exemple, dans le cas où
et leur ordre de
dégénérescence. Ces valeurs propres peuvent être classées par valeurs
décroissantes en indiquant sous chacune son ordre de dégénérescence.
Soit, par exemple, dans le cas où
![]() :
:
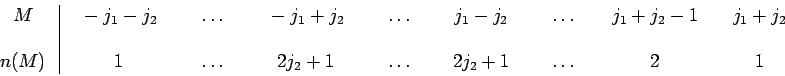 |
La valeur maximale de ![]() est
est ![]() . C'est donc également celle de :
. C'est donc également celle de :
A chaque valeur de ![]() , en commençant par la plus grande, correspond une
série de
, en commençant par la plus grande, correspond une
série de ![]() valeurs
valeurs ![]() avec
avec
![]() conformément à la
remarque
conformément à la
remarque ![]() précédente. Il en résulte que les valeurs successives
de
précédente. Il en résulte que les valeurs successives
de ![]() sont les suivantes :
sont les suivantes :
|
|
et qu'aucune de ces valeurs de ![]() n'est dégénérée.
n'est dégénérée.
Dans chacun des sous-espaces associés à une valeur de ![]() bien déterminée, un seul vecteur correspond à un couple de
valeurs
bien déterminée, un seul vecteur correspond à un couple de
valeurs ![]() : le vecteur
: le vecteur
![]() . Les
observables
. Les
observables ![]() et
et ![]() peuvent donc remplacer les
observables
peuvent donc remplacer les
observables ![]() et
et ![]() . Nous obtenons donc deux E.C.O.C.
et les bases correspondantes :
. Nous obtenons donc deux E.C.O.C.
et les bases correspondantes :
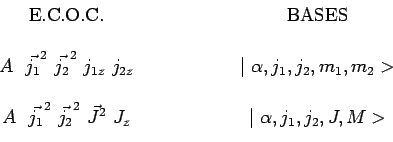 |
En fait ici les valeurs ![]() et
et ![]() sont supposées bien déterminées et
constantes.
sont supposées bien déterminées et
constantes.