suivant monter précédent table des matières
suivant: Principe de Pauli monter: Le postulat VIII (principe précédent: c) Dégénérescence d'échange   Table des matières

Symétrie et antisymétrie des états

Or, nous savons que cette dégénérescence d'échange n'a aucune signification physique, les $ n!$ kets $ \mathcal{P}\,\mid \Psi_a>$ considérés ci-dessus, ou plus généralement les $ n!$ kets $ \mathcal{P}\,\mid \Psi>$ quel que soit $ \mid \Psi>$ doivent en fait décrire un seul et même état physique, et ceci quelle que soit l'une $ \mathcal{P}$ des $ n!$ permutations indépendantes. Or, conformément au postulat I, cet état unique doit être représenté par un vecteur ket $ \mid \Psi>$ ou ses multiples. Il en résulte que ce ket représentatif, s'il est normé, doit à un facteur de phase près, être invariant sous l'effet de toutes les permutations induites, soit :

\begin{displaymath}\begin{array}{\vert c\vert}\hline { }\\ ~~\mathcal{P}\,\mid \... ...nd{array}~~~~~~~~~~~~~~~~~~~~~~~~\mathcal{P}\,\in\,\mathbb{P}_n\end{displaymath}      

$ \mathbb{P}_n$ désignant le groupe des permutations des $ n$ premiers entiers. Nous allons voir que la contrainte précédente va suffire pour déterminer univoquement le ket $ \mid \Psi>$ . A cet effet, il y a lieu d'établir la suite des théorèmes suivants :

Théorème 1  


Si $ P$ désigne une transposition : $ P=P_{ij}=(i\longleftrightarrow j)=(i,j)$ alors $ \mathcal{P}\,\mid \Psi>=\pm\,\mid \Psi>$ .


En effet : $ ~~~~~~P^2=(i,j)(i,j)=1~~~~~$ et si $ ~~~~~\mathcal{P}\,\mid \Psi>=C\,\mid \Psi>~~~~~$ alors :


$ ~~~~~~\mathcal{P}^2\,\mid \Psi>=C\,\mathcal{P}\,\mid \Psi>=C^2\,\mid \Psi>~~~~~~$ et : $ ~~~~~~C=\pm1=\varepsilon(i,j)~~~~~~$

Théorème 2  


Une même valeur de $ \varepsilon$ est associée à toutes les transpositions.


En effet : $ ~~~~(k,l)=(j,k)(i,k)(i,j)(j,l)(i,k)~~~~$ d'où il résulte :

$\displaystyle \varepsilon(k,l)$ $\displaystyle =$ $\displaystyle \varepsilon(j,l)^2\,\varepsilon(i,k)^2\,\varepsilon(i,j) ~=~ \varepsilon(i,j)$  

et soit $ \varepsilon$ cette valeur commune.

Théorème 3   Tout état physique d'un ensemble de $ n$ particules identiques doit être représenté par un vecteur ket symétrique ou antisymétrique.

En effet, toute permutation $ P$ peut être décomposée un produit de $ p(P)$ transpositions, ce nombre $ p(P)$ étant défini à un nombre pair additif près. La parité de $ p$ s'appelle la parité de la permutation. On en déduit alors :

$\displaystyle \mathcal{P}\,\mid \Psi>=\varepsilon^{p(P)}\,\mid \Psi>$      

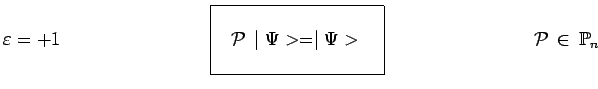
Si $ \varepsilon=+1~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}\hline { }\\ ... ... { }\\ \hline \end{array}~~~~~~~~~~~~~~~~~~~~~~~~\mathcal{P}\,\in\,\mathbb{P}_n$

on dit alors que l'état $ \Psi$ est symétrique.

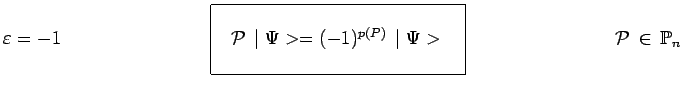
Si $ \varepsilon=-1~~~~~~~~~~~~~~~~~~~~~~~~\begin{array}{\vert c\vert}\hline { }\\ ... ... { }\\ \hline \end{array}~~~~~~~~~~~~~~~~~~~~~~~~\mathcal{P}\,\in\,\mathbb{P}_n$

et on dit alors que l'état $ \Psi$ est antisymétrique.

Théorème 4   Au même instant ``$ t$ '', tous les états d'un ensemble de particules identiques sont tous en même temps symétriques ou tous antisymétriques.

En effet, cette propriété est une conséquence nécessaire du principe de superposition car une combinaison quelconque, c'est-à-dire un mélange d'états symétriques, et d'états antisymétriques n'est plus lui-même ni symétrique ni antisymétrique, contrairement à la conclusion du Théorème 3.

Théorème 5   Cette propriété de symétrie ou d'antisymétrie, commune à tous les états possibles, au même instant $ t$ d'un ensemble de particules identiques ne dépend pas de $ t$ . Elle est conservée au cours de l'évolution du système. Cette propriété de symétrie ou d'antisymétrie est donc une propriété du système.

En effet, comme toute autre observable d'un ensemble de particules interchangeables, le hamiltonien est un opérateur symétrique invariant sous l'effet des permutations induites $ \mathcal{P}$ , d'où résulte comme nous l'avons déjà remarqué précédemment :

$\displaystyle \mathcal{P}\,H\,\mathcal{P}^{-1}=H~~~~~~~~\mathrm{et}~~~~~~~~ \left[\mathcal{P},H\right]=0$      

et puisque l'opérateur d'évolution ne dépend que de $ H$ :

$\displaystyle \mathcal{U}(t,t_0)=e^{-\frac{i}{\hbar}\,(t-t_0)\,H}~~~~~~~~\mathrm{et~donc} ~~~~~~~~\left[\mathcal{P},\mathcal{U}(t,t_0)\right]=0$      

Si donc $ \mathcal{P}\,\mid \Psi(t_0)>=\varepsilon\,\mid \Psi(t_0)>$ alors :

$\displaystyle \mathcal{P}\,\mid \Psi(t)>=\mathcal{P}\,\mathcal{U}(t,t_0)\,\mid \Psi(t_0)>= \mathcal{U}(t,t_0)\,\mathcal{P}\,\mid \Psi(t_0)>$      


$\displaystyle \mathcal{P}\,\mid \Psi(t)>=\varepsilon\,\mid \Psi(t)>$      

La valeur de $ \varepsilon$ est donc conservée au cours du temps. Il en résulte que tout opérateur $ \mathcal{P}$ de permutation induite est une constante du mouvement.

Question 5-5 : Montrez que $ \mathcal{P}$ demeure une constante du mouvement lorsque le hamiltonien dépend du temps.

suivant monter précédent table des matières
suivant: Principe de Pauli monter: Le postulat VIII (principe précédent: c) Dégénérescence d'échange   Table des matières
Arnaud Balandras 2005-04-02