Pour un ensemble de particules identiques et de spin entier, la fonction d'onde
globale ![]() doit être symétrique, c'est-à-dire invariante sous l'effet de
n'importe quelle permutation induite
doit être symétrique, c'est-à-dire invariante sous l'effet de
n'importe quelle permutation induite
![]() , et donc telle que :
, et donc telle que :
Ici encore, si
![]() désignent une suite d'états à une particule, le ket :
désignent une suite d'états à une particule, le ket :
qui représente un état du système global dans lequel la
première particule est dans l'état
![]() , la seconde
dans l'état
, la seconde
dans l'état
![]() ,... la
,... la
![]() dans l'état
dans l'état
![]() :
:
ne peut correspondre à un état physique, car cet état n'est pas
symétrique. Effectuer une permutation ![]() sur les particules revient à
effectuer une permutation sur les états :
sur les particules revient à
effectuer une permutation sur les états :
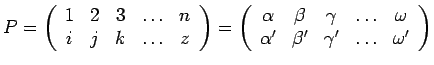 |
et le nouveau ket ainsi obtenu :
représente le même état physique.
Ainsi, l'état physique semblerait pouvoir être représenté par une
combinaison linéaire quelconque du type :
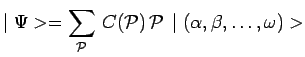 |
![]() désignant une constante dépendant de
désignant une constante dépendant de
![]() .
.
Le principe de Pauli, déjà justifié précédemment, lève
cet arbitraire (cf. dégénérescence d'échange) et précise
que la seule combinaison linéaire valable est celle qui a
pour effet de rendre
![]() symétrique, c'est-à-dire invariant
sous l'effet des permutations induites. On vérifie aisément
que cette combinaison symétrique est celle qui est obtenue dans
le développement du même déterminant de Slater que
précédemment :
symétrique, c'est-à-dire invariant
sous l'effet des permutations induites. On vérifie aisément
que cette combinaison symétrique est celle qui est obtenue dans
le développement du même déterminant de Slater que
précédemment :
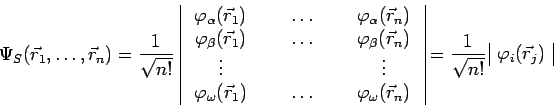 |
en convenant toutefois que dans le développement du
déterminant, chaque terme soit précédé du signe +, ce qui revient
à écrire :
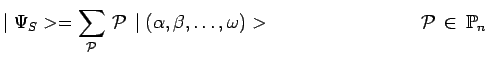 |