Spin et statistique

La statistique étudie la manière dont les particules d'un ensemble viennent occuper les états physiques qui leur sont proposés. Or nous venons de voir que la nature des états, et les règles d'occupation, dépendent du spin de ces particules.

Si le spin des particules identiques de cet ensemble est demi-entier, les seuls états possibles du système sont antisymétriques, et par voie de conséquence les états individuels occupés sont nécessairement linéairement indépendants. La statistique particulière qui en résulte a été étudiée par Fermi et Dirac et pour cette raison ces particules de spin demi-entier (électrons, protons, neutrons,... etc) sont appelés des fermions.

Si le spin des particules identiques de cet ensemble est entier, les seuls états possibles du système sont symétriques. Les états individuels occupés peuvent être linéairement dépendants et même identiques. La statistique particulière qui en résulte a été étudiée par Bose et Einstein, et pour cette raison ces particules de spin entier s'appelle des bosons.

Le principe de Pauli peut alors s'énoncer brièvement comme suit :

$\imath-$ Le vecteur ket (ou la fonction d'onde) représentatif d'un ensemble de fermions identiques est antisymétrique.

$\imath\imath-$ Le vecteur ket (ou la fonction d'onde) représentatif d'un ensemble de bosons identiques est symétrique.

Afin d'illustrer simplement la différence de comportement des fermions et des bosons, considérons par exemple un système de deux particules 1 et 2 identiques n'admettant que deux états indépendants $\mid a>$ et $\mid b>$ et en équilibre thermodynamique avec un milieu ambiant à très haute température. Dans ces conditions, la mécanique quantique, comme la mécanique classique d'ailleurs, indique que les probabilités d'occupation de chacun des états possibles sont toutes égales entre elles.

Si donc les deux particules obéissaient à la statistique classique de Maxwell-Boltzmann, les états possibles seraient, en indiquant dans l'ordre l'état occupé par la première particule suivi de l'état occupé par la seconde :

$$\mid a,a>~,~\mid a,b>~,~\mid b,a>~,~\mid b,b>$$

affectés chacun d'une probabilité de réalisation égale à $\frac{1}{4}$ . Ainsi en particulier, la probabilité de trouver les deux particules dans le même état est égale à $\frac{1}{2}$ .

Si les deux particules sont des fermions, le seul état possible est l'état antisymétrique :

$$\frac{1}{\sqrt{2}}\,(\mid a,b>-\mid b,a>)$$

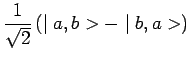et la probabilité de trouver les deux particules dans le même état est nulle.

Enfin, si les deux particules sont des bosons, les états possibles distincts et indépendants sont des états symétriques :

$$\mid a,a>~,~\frac{1}{\sqrt{2}}\,(\mid a,b>+\mid b,a>)~,~\mid b,b>$$

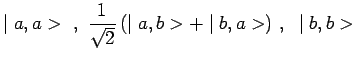et la probabilité de trouver les deux particules dans le même état $\mid a>$ ou $\mid b>$ est $\frac{1}{3}+\frac{1}{3}=\frac{2}{3}$ .

Ainsi la probabilité de trouver les deux particules dans le même état est égale à zéro pour des fermions, $\frac{1}{2}$ pour des particules classiques et $\frac{2}{3}$ pour des bosons. Les statistiques de Bose et Fermi s'écartent en sens inverse de la statistique classique.

Par rapport au comportement prévu par la mécanique classique, on peut dire, en ce sens, que les fermions ont tendance à se disperser et les bosons à se grouper.