suivant monter précédent table des matières
suivant: Deuxième forme du paradoxe monter: La mécanique quantique est-elle précédent: La mécanique quantique est-elle   Table des matières

a) Première forme du paradoxe

Considérons un système physique $ \mathbb{S}$ composé lui-même de deux systèmes physiques A et B, en interaction (deux particules par exemple) :

$\displaystyle \mathbb{S}=\mathcal{A}\oplus\,\mathcal{B}$      

Soit $ A$ et $ A^\prime$ deux E.C.O.C. distincts de $ \mathcal{A}$ et $ B$ un E.C.O.C. de $ \mathcal{B}$ , admettant pour vecteurs et valeurs propres :

$\displaystyle A\,\mid \alpha>=\alpha\,\mid \alpha>~~~~~~~~~~~~~~~~~~~~~~~~A^\prime\,\mid \alpha^\prime>^\prime=\alpha^\prime\,\mid \alpha^\prime>^\prime$      


$\displaystyle B\,\mid \beta>=\beta\,\mid \beta>$      

$ A$ et $ B$ d'une part, $ A^\prime$ et $ B$ d'autre part constituent deux E.C.O.C. de $ \mathbb{S}$ V6 de telle sorte que pour tout état $ \Psi$ de $ \mathbb{S}$ :

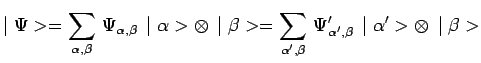$\displaystyle \mid \Psi>=\sum\limits_{\alpha,\beta}\,\Psi_{\alpha,\beta}\,\mid ... ...ta}\,\Psi^\prime_{\alpha^\prime,\beta}\,\mid \alpha^\prime>\otimes\,\mid \beta>$      

Considérons le système à un instant $ t$ postérieur à l'interaction et donc quand les deux sous-systèmes $ \mathcal{A}$ et $ \mathcal{B}$ sont séparés spatialement.

Si à cet instant $ t$ on mesure les observables $ A$ sur $ \mathcal{A}$ on trouve un résultat $ A=\alpha_0$ et le ket représentatif de l'état du système $ \mathbb{S}$ devient après application du postulat IV (réduction du paquet d'ondes) :

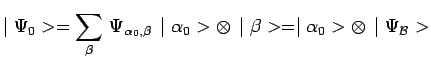$\displaystyle \mid \Psi_0>=\sum\limits_{\beta}\,\Psi_{\alpha_0,\beta}\,\mid \alpha_0>\otimes\,\mid \beta> =\mid \alpha_0>\otimes\,\mid \Psi_\mathcal{B}>$      

avec :

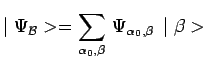$\displaystyle \mid \Psi_\mathcal{B}>=\sum\limits_{\alpha_0,\beta}\,\Psi_{\alpha_0,\beta}\,\mid \beta>$      

Mais si, à ce même instant $ t$ on mesure les observables $ A^\prime$ , on trouve le résultat $ A^\prime=\alpha_0^\prime$ et le ket représentatif de l'état de $ \mathbb{S}$ s'écrit :

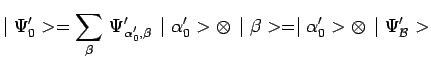$\displaystyle \mid \Psi_0^\prime>=\sum\limits_{\beta}\, \Psi^\prime_{\alpha_0^\... ...times\,\mid \beta> =\mid \alpha_0^\prime>\otimes\,\mid \Psi^\prime_\mathcal{B}>$      

avec :

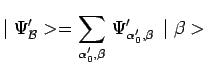$\displaystyle \mid \Psi^\prime_\mathcal{B}>=\sum\limits_{\alpha_0^\prime,\beta}\, \Psi^\prime_{\alpha_0^\prime,\beta}\,\mid \beta>$      

et on remarque aussitôt :

$\displaystyle \mid \Psi_\mathcal{B}>\not=\mid \Psi^\prime_\mathcal{B}>$      

Or, à l'instant $ t$ , les deux systèmes $ \mathcal{A}$ et $ \mathcal{B}$ étant séparés par un intervalle du genre espace, constituent deux systèmes réels indépendants. Le système $ \mathcal{B}$ (une particule $ \mathcal{B}$ par exemple) constitue lui-même un élément de réalité, dont l'état à l'instant $ t$ ne peut pas dépendre de la mesure effectuée sur le système $ \mathcal{A}$ . Par conséquent, conformément au critère énoncé ci-dessus, cet état physique bien déterminé de $ \mathcal{B}$ devrait au moins être représenté si la mécanique quantique était complète, par un vecteur ket bien déterminé et donc unique. Or, nous venons de trouver deux vecteurs kets distincts $ \mid \Psi_\mathcal{B}>$ et $ \mid \Psi^\prime_\mathcal{B}>$ candidats pour représenter l'état du système $ \mathcal{B}$ . En fait, il en existe même autant que l'on veut (associés aux E.C.O.C. $ A$ , $ A^\prime$ , $ A^{\prime\prime}$ ,... etc) candidats tous aussi légitimes les uns que les autres, pour représenter le même état de $ \mathcal{B}$ , et donc en contradiction avec l'exigence d'une description biunivoque et complète.

suivant monter précédent table des matières
suivant: Deuxième forme du paradoxe monter: La mécanique quantique est-elle précédent: La mécanique quantique est-elle   Table des matières
Arnaud Balandras 2005-04-02