Deuxième forme du paradoxe

Considérons deux particules $\mathcal{P}$ et $\mathcal{P}^\prime$ de coordonnées $X_i$ et $X_j^\prime$ et d'impulsions $P_i$ et $P_j^\prime$ (avec $i,j=1,2,3$ ). Les observables :

$$\bar{X}_i=X_i-X_i^\prime~~~~~~~~~~~~\mathrm{et}~~~~~~~~~~~~ \bar{... ...\prime~~~~~~~~~~~~ \left\lbrace\begin{array}{c}i\\ j\\ \end{array}=1,2,3\right.$$

$$\left[\bar{X}_i,\bar{P}_j\right]= \left[X_i,P_j\right]-[{X_i^\prime},{P_j^\prime}]= i\hbar\,(\delta_{ij}-\delta_{ij})=0$$

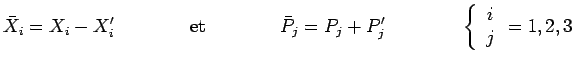commutent et admettent donc un ensemble de vecteurs propres communs $\{\mid x,p>\}$ tels que :

$$\bar{X}_i\,\mid x,p>=\bar{x}_i\,\mid x,p>~~~~~~~~~~~~~~~~~~~~~~~~\bar{P}_j\,\mid x,p>=\bar{p}_j\,\mid x,p>$$

Considérons donc, à un instant $t$ , un état des deux particules représenté par un tel vecteur ket :

$$\mid x,p>$$

On va montrer que, sans agir sur la particule $\mathcal{P}$ , et donc sans la perturber en aucune façon, nous pouvons prédire avec certitude les valeurs à cet instant $t$ de ses coordonnées $X_i$ et celles des composantes $P_j$ de son impulsion. En effet pour cela, il suffit d'effectuer à l'instant $t$ la mesure de ces mêmes quantités soit $X_i^\prime$ soit $P_j^\prime$ sur la particule $\mathcal{P}^\prime$ :

$$\mathrm{Si}~~~~~~~~X_i^\prime=x_i^\prime~~~~~~~~X_i=\bar{X}_i+X_i^\prime ~~~~~~~~\mathrm{et}~~~~~~~~x_i=\bar{x}_i+x_i^\prime$$

$$\mathrm{Si}~~~~~~~~P_j^\prime=p_j^\prime~~~~~~~~P_j=\bar{P}_j-P_j^\prime ~~~~~~~~\mathrm{et}~~~~~~~~p_j=\bar{p}_j-p_j^\prime$$

A cet instant $t$ , la position $(x_i)$ et l'impulsion $(p_j)$ de la particule $\mathcal{P}$ sont donc prévisibles avec certitude l'une et l'autre (mais non l'une avec l'autre). Ces valeurs $(x_i)$ et $(p_j)$ ne peuvent toutefois dépendre des mesures, effectuées ou non effectuées, sur l'autre particule $\mathcal{P}^\prime$ (postulat de séparabilité). Conformément au critère de réalité ces valeurs constituent donc des éléments de réalité physique possédés en même temps par la particule $\mathcal{P}$ . Dans l'état correspondant, la position $X_i$ et l'impulsion $P_j$ de cette particule $\mathcal{P}$ sont donc simultanément définies :

$$X_i=x_i~~~~~~~~~~~~~~~~~~~~~~~~P_j=p_j~~~~~~~~~~~~~~~~~~~~~~~~(i,j=1,2,3)$$

Selon le formalisme quantique, un tel état physique devrait être représenté par un vecteur propre simultané des observables $X_i$ et $P_j$ . Or un tel vecteur n'existe pas^V7, puisque le commutateur de $X_i$ et $P_j$ est égal à $i\hbar\,\delta_{ij}$ . Tout ceci semble indiquer que les vecteurs kets du formalisme quantique ne codent qu'une partie seulement des propriétés des états physiques réels. La représentation quantique est donc incomplète.