Le calcul des intégrales de chemin précédentes parait
une entreprise formidable. Heureusement, hormis les
situations microscopiques qui font intervenir les dimensions
atomiques, les valeurs de
![]() , comparées à
, comparées à
![]() , sont gigantesques et varient rapidement
(
, sont gigantesques et varient rapidement
(
![]() ) pour deux chemins
) pour deux chemins ![]() et
et ![]() très
voisins, de telle sorte que ces chemins peuvent être appariés
de telle manière que la différence de phase
très
voisins, de telle sorte que ces chemins peuvent être appariés
de telle manière que la différence de phase ![]() soit égale
à
soit égale
à
![]() et que la somme de leurs contributions soit
nulle.
et que la somme de leurs contributions soit
nulle.
Les seules contributions effectives à l'intégrale proviennent alors des chemins pour lesquels la phase est stationnaire, c'est-à-dire pour lesquels la dérivée s'annule. Ces chemins sont donc ceux pour lesquels l'action est extremum. Ces chemins stationnaires sont précisément les trajectoires classiques révélées par le principe de moindre action.
|
|
avec :
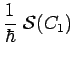 |
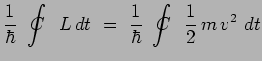 |
mais :
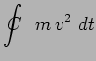 |
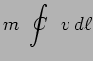 |
ce qui est l'expression du principe de Maupertuis, ou
encore :
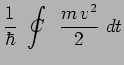 |
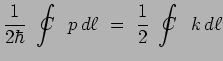 |
||
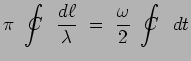 |
ce qui constitue l'expression du principe de Huygens.
De l'expression de ![]() se déduit la structure de la figure
d'interférence :
se déduit la structure de la figure
d'interférence :
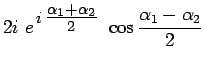 |
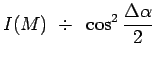 |
![$\displaystyle \cos^2\left[\pi~\frac{\ell_1-\ell_2}{\lambda}\right]~~~~~~~~~~~~~~~(\Delta\alpha\,=\,\alpha_1-\alpha_2)$](img4132.png) |
On retrouve bien les expressions familières faisant apparaître
la différence
![]() des deux chemins
des deux chemins ![]() et
et ![]() ,
comparée à la longueur d'onde
,
comparée à la longueur d'onde ![]() .
.