On va considérer ci-après l'évolution d'une particule quantique, et pour simplifier les notations (mais seulement les notations), on la supposera placée dans un espace à une seule dimension.
Conformément aux postulats de la mécanique quantique non relativiste,
l'amplitude de probabilité de localiser cette particule au point
![]() , à l'instant
, à l'instant ![]() , sachant qu'elle aurait déjà été
localisée au point
, sachant qu'elle aurait déjà été
localisée au point ![]() à un instant antérieur
à un instant antérieur ![]() ,
a pour expression :
,
a pour expression :
le signe de proportionnalité ![]() tenant compte de
la non renormalisabilité des états propres associés à des
valeurs propres continues.
tenant compte de
la non renormalisabilité des états propres associés à des
valeurs propres continues.
Dans la représentation de Heisenberg :
d'où :
Il en résulte immédiatement :
Il y a lieu de faire ici deux remarques utiles pour la suite :
![]() L'expression de l'opérateur unité dans la
représentation de Heisenberg se déduit immédiatement de son
expression dans la représentation de Schrödinger :
L'expression de l'opérateur unité dans la
représentation de Heisenberg se déduit immédiatement de son
expression dans la représentation de Schrödinger :
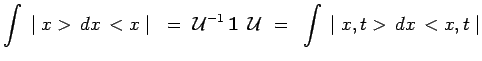 |
![]() L'amplitude de probabilité de localiser la
particule au point
L'amplitude de probabilité de localiser la
particule au point ![]() à l'instant
à l'instant ![]() n'est rien d'autre que la
fonction d'onde de Schrödinger dans sa propre représentation :
n'est rien d'autre que la
fonction d'onde de Schrödinger dans sa propre représentation :
|
|
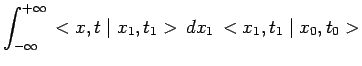 |
qui peut encore s'écrire :
 |
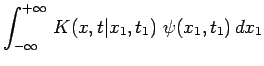 |
|
|
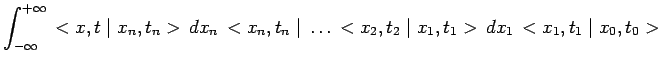 |
Le principe de Feynman postule l'expression de l'amplitude partielle :
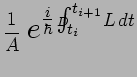 |
![]() désignant une constante nécessaire à la
renormalisation et qui reste à déterminer. On remarque que
l'exposant de l'exponentielle fait apparaître l'intégrale
d'action calculée sur la droite d'Univers qui joint les deux
événements considérés.
désignant une constante nécessaire à la
renormalisation et qui reste à déterminer. On remarque que
l'exposant de l'exponentielle fait apparaître l'intégrale
d'action calculée sur la droite d'Univers qui joint les deux
événements considérés.
En choisissant équidistants les instants ![]() soit :
soit :
![]() et en remplaçant par son
expression chacune des amplitudes partielles qui figure dans
l'intégrale précédente, on obtient :
et en remplaçant par son
expression chacune des amplitudes partielles qui figure dans
l'intégrale précédente, on obtient :
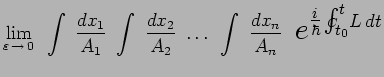 |
On notera le caractère très singulier de cette intégrale
portant sur une infinité de variables ![]() , puisque chacune de
ces variables est associée à un instant
, puisque chacune de
ces variables est associée à un instant ![]() et que ce nombre
d'instants devient infini en même temps que
et que ce nombre
d'instants devient infini en même temps que
![]() . Cette intégrale est calculée sur
chacune des lignes d'Univers qui connecte la suite des
événements
. Cette intégrale est calculée sur
chacune des lignes d'Univers qui connecte la suite des
événements
![]() . Les
constantes
. Les
constantes ![]() désignent des constantes nécessaires à la
normalisation.
désignent des constantes nécessaires à la
normalisation.
L'expression intégrale précédente peut encore s'écrire
symboliquement :
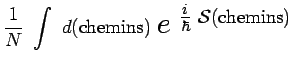 |
avec :
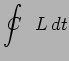 |
ou encore plus schématiquement :
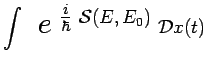 |
Finalement, la probabilité de la transition qui connecterait
l'événement ![]() à l'événement ultérieur
à l'événement ultérieur ![]() a pour
expression :
a pour
expression :