Exemples d'application du principe de Feynman

Il vaut la peine de signaler ici un phénomène expérimental remarquable et prévu par Bohm et Aharonov. Plaçons entre les deux fentes $F_1$ et $F_2$ et parallèlement à elles un très long et très fin solénoïde $s$ parcouru par un courant. Le champ électromagnétique ainsi créé est purement interne au solénoïde et ne semble pas capable d'agir sur les électrons toujours extérieurs à ce solénoïde. Cependant on constate néanmoins un déplacement des franges quand le solénoïde est alimenté.

Cet effet Bohm-Aharonov peut être expliqué de la manière suivante. Il y a lieu d'introduire dans la fonction de Lagrange le terme supplémentaire dû à la présence du champ électromagnétique :

$$L = \frac{1}{2}\,m\,v^2 + \frac{q}{c}\,\left(\vec{A}\cdot\vec{v} - V\right)$$

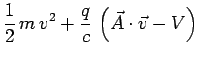Ce terme complémentaire introduit un déphasage supplémentaire qui, dans la jauge de Coulomb $V\,\equiv\,0$ , s'écrit simplement :

$$\beta = \frac{1}{\hbar}~\int_{~~}^{~~}\hspace{-.70cm}C\hspace{.30cm}\frac... ...}~~~~~~~~~~~~~~~~~~~~~~~~\left(q\hspace{-.17cm}/\,\,=\,\frac{q}{\hbar c}\right)$$

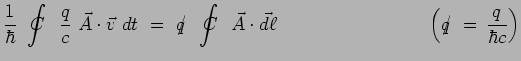La prise en compte des deux chemins $C_1$ et $C_2$ introduit alors une différence de phase additionnelle $\Delta\beta$ qui s'ajoute à $\Delta\alpha$ :

$$\Delta\beta = \beta_1-\beta_2 ~=~ q\hspace{-.17cm}/\,~\left[\int_{~~}^{~~}\hspa... ...cm}C_2\hspace{.30cm}\right]~=~q\hspace{-.17cm}/\,~\oint~\vec{A}\cdot\vec{d\ell}$$

Cette dernière intégrale porte sur le contour fermé constitué de $C_1$ et $C_2$ parcouru en sens inverse de $M$ vers $S$ . Par application du théorème de Stokes, on peut encore écrire :

$$\Delta\beta = q\hspace{-.17cm}/\,~\int\int_S\,\overrightarrow{rot}\,\vec{A}\cdo... ...m}/\,~\int\int_S\,\vec{B}\cdot\overrightarrow{dS} ~=~ q\hspace{-.17cm}/\,\,\Phi$$

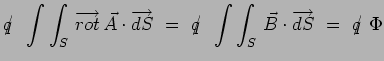$\Phi$ désignant le flux magnétique à l'intérieur du solénoïde $s$ . L'intensité au point $M$ dépend donc de $\Phi$ :

$$I(M) ~\div~ \cos^2\frac{\Delta\alpha+\Delta\beta}{2} = \cos^2\left(\pi\,\frac{\Delta\ell}{\lambda} + q\hspace{-.17cm}/\,\,\frac{\Phi}{2}\right)$$

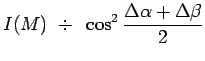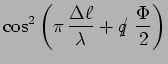et on comprend alors pourquoi le positionnement des franges d'interférence dépend de $\Phi$ .