Nous nous proposons de calculer l'amplitude de probabilité de
localiser une particule libre au point ![]() à l'instant
à l'instant ![]() ,
sachant qu'elle avait été localisée au point
,
sachant qu'elle avait été localisée au point ![]() à
l'instant
à
l'instant ![]() :
:
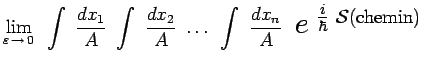 |
![]() désignant l'intégrale
d'action calculée sur le chemin qui joint les points
désignant l'intégrale
d'action calculée sur le chemin qui joint les points
![]()
![]() avec :
avec :
 |
et puisque la particule est libre :
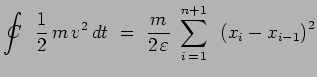 |
L'expression calculée porte sur un produit de fonctions
gaussiennes dont les intégrales sont elles-mêmes gaussiennes
de telle sorte que les intégrales, toutes gaussiennes, peuvent
s'effectuer l'une après l'autre :
![$\displaystyle \frac{1}{A}~\int_{-\infty}^{+\infty}\,{\scalebox{1.6}{$e$}}^{\sca...
...\,\varepsilon}$}~\scalebox{1.0}{$\left[(x_2-x_1)^2 + (x_1-x_0)^2\right]$}}~dx_1$](img4155.png) |
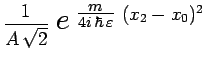 |
En multipliant le second membre par :
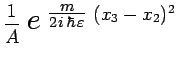 |
et en intégrant sur ![]() , on obtient une expression
encore semblable au résultat de la première intégration sur
, on obtient une expression
encore semblable au résultat de la première intégration sur
![]() mais avec
mais avec
![]() au lieu de
au lieu de
![]() et
et
![]() au lieu de
au lieu de
![]() . En procédant ainsi par
récurrence, on obtient finalement :
. En procédant ainsi par
récurrence, on obtient finalement :
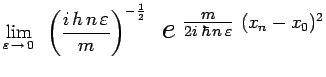 |
et puisque :
et avec
![]() :
:
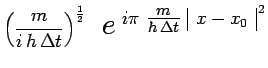 |
On retrouve bien un résultat antérieur qui donne l'expression du propagateur non relativisteVII1.