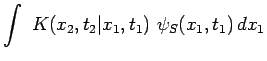De Feynman à Schrödinger

Nous nous proposons de montrer comment le principe de Feynman conduit à l'équation de Schrödinger. A cet effet, il est commode d'écrire ce principe sous la forme :

$$\psi_S(x_2,t_2) = \int~K(x_2,t_2 \vert x_1,t_1)~\psi_S(x_1,t_1)\,dx_1$$

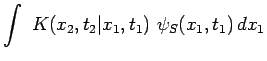avec :

$$K(x_2,t_2 \vert x_1,t_1) = <x_2,t_2 \mid x_1,t_1> ~=~ \frac{1}{A}~e^{~\frac{i}{\hbar}\,\mathcal{S}}$$

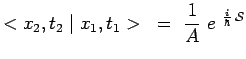et :

$$\mathcal{S} = \int_{x_1,t_1}^{x_2,t_2}\,L(x,\dot{x},t)~dt$$

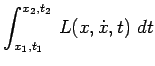Considérons des intervalles d'espace et de temps infinitésimaux avec :

$$x_2 = x~~~~~~~~~~~~~~~~~~~~~~~~x_1 ~=~y~=~x+\eta~~~~~~~~~~~~~~~~~~~~~~~~t_1~=~t~=~t_2-\varepsilon$$

Les expressions précédentes deviennent alors :

$$\psi(x,t+\varepsilon) = \frac{1}{A}~\int_{-\infty}^{+\infty}\,exp\left[\frac{i}{\hbar}~\v... ...ilon~L\,\left(\frac{x+y}{2},\frac{x-y}{\varepsilon}\right) \right]~\psi(y,t)~dy$$

avec, dans le cas d'une particule de masse $m$ et plongée dans un potentiel $V$ :

$$L = K - V ~=~ \frac{1}{2}\,m\,v^2 - V(x) ~=~ \frac{m}{2}\,\left(\frac{x-y}{\varepsilon}\right)^2- V\left(\frac{x+y}{2}\right)$$

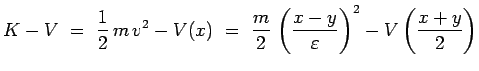de telle sorte que :

$$\psi(x,t+\varepsilon) = \frac{1}{A}~\int_{-\infty}^{+\infty}\,e^{\scalebox{1.0}{$~\frac{i... ...\,\varepsilon} - \varepsilon\,V(x+\frac{\eta}{2})\right]$}} ~\psi(x+\eta)~d\eta$$

et pour $\varepsilon\,\to\,0~$ et $~\eta\,\to\,0$ :

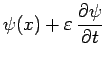$$\psi(x) + \varepsilon\,\frac{\partial\psi}{\partial t} = \frac{1}{A}~\int_{-\infty}^{+\infty}\,e^{\scalebox{1.0}{$~\frac{i... ...artial x} + \frac{\eta^2}{2}\,\frac{\partial^2\psi}{\partial x^2}~\right]~d\eta$$

En identifiant le coefficient de $\psi(x)$ dans les deux membres, on détermine la valeur de la constante d'intégration $A$ :

$$\frac{1}{A}~\int_{-\infty}^{+\infty}\,e^{\scalebox{1.0}{$~\frac{i}{\hbar}~\frac{m\,\eta^2}{2\,\varepsilon}$}}~d\eta = 1~~~~~~~~~~~~\mathrm{d'o\grave{u}}~~~~~~~~A~=~\left(\frac{i\,h\,\varepsilon}{m}\right)^{\frac{1}{2}}$$

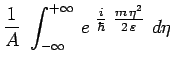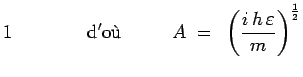et tenu compte des résultats mathématiques suivants :

$$\int_{-\infty}^{+\infty}\,e^{\scalebox{1.0}{$~\frac{i}{\hbar}~\frac{m\,\eta^2}{2\,\varepsilon}$}}~\eta~d\eta = 0~~~~~~~~~~~~~~~~~\mathrm{et}~~~~~~~~~~~~~~~~ \frac{1}{A}~\int_{-... ...{m\,\eta^2}{2\,\varepsilon}$}}~\eta^2~d\eta ~=~ \frac{i\,\hbar\,\varepsilon}{m}$$

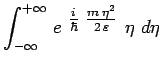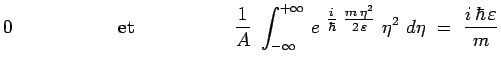on obtient :

$$\psi + \varepsilon\,\frac{\partial\psi}{\partial t} = \left(1-\frac{i}{\hbar}\,\varepsilon\,V\right)\,\psi + \frac{i\,\hbar\,\varepsilon}{2m}\,\frac{\partial^2\psi}{\partial x^2}$$

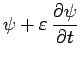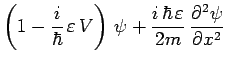et finalement l'équation de Schrödinger :

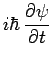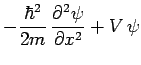$$i\hbar\,\frac{\partial\psi}{\partial t} = -\frac{\hbar^2}{2m}\,\frac{\partial^2\psi}{\partial x^2} + V\,\psi$$