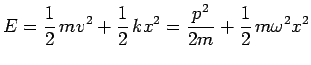B) Hamiltonien

Conformément au principe de Born, l'énergie d'un tel oscillateur linéaire ne peut prendre pour valeur que l'une des valeurs propres de son observable énergie, encore appelée hamiltonien. Il s'agit donc d'abord de construire cet opérateur et d'en calculer ensuite les valeurs propres.

L'énergie totale de l'oscillateur harmonique à une dimension admet l'expression classique :

$$E=\frac{1}{2}\,mv^2+\frac{1}{2}\,kx^2=\frac{p^2}{2m} + \frac{1}{2}\,m\omega^2x^2$$

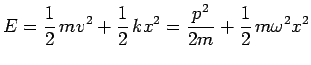d'où on déduit immédiatement l'expression quantique du hamiltonien, fonction des observables $P$ et $X$ ^I35 :

$$H=\frac{1}{2m}\,P^2 + \frac{1}{2}\,m\omega^2\,X^2$$

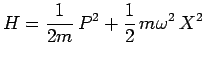C'est une fonction des observables position et impulsion. Nous verrons plus loin que ces deux observables ne commutent pas et que leur commutateur a pour valeur :

$$[X,P]=i\,\hbar$$

Nous allons constater ici, comme dans le cas des moments angulaires, que cette relation de commutation suffit pour déterminer les valeurs propres et les vecteurs propres du hamiltonien.

Pour simplifier les notations, il est commode de poser :

$$\mathcal{Q}=\sqrt{\frac{m\omega}{\hbar}}\,X ~~~~~~~~~~~~~~~~~~~~~... ...thrm{et} ~~~~~~~~~~~~~~~~~~~~~~~~\mathcal{P} = \frac{1}{\sqrt{m\hbar\omega}}\,P$$

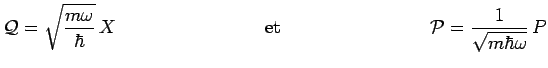L'hamiltonien s'écrit alors :

$$\begin{array}{ccl} H & = & \scalebox{1.4}{$\frac{\hbar\omega}... ...mathcal{P})-i\,[\mathcal{Q},\mathcal{P}]\right) \\ \end{array}$$

Tenu compte de la relation de commutation :

$$[\mathcal{Q},\mathcal{P}]=\hbar^{-1}\,[X,P]=i$$

et définissant un nouvel opérateur :

$$\eta = \frac{1}{\sqrt{2}}\,(\mathcal{Q}+i\,\mathcal{P}) ~~~~~~~~~... ...~~~~~~~~~~~~~~~ \eta^\dagger = \frac{1}{\sqrt{2}}\,(\mathcal{Q}-i\,\mathcal{P})$$

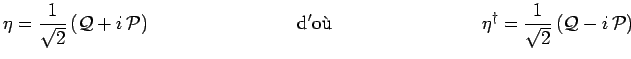l'hamiltonien peut finalement s'écrire :

$$H = \hbar\omega~(\eta^\dagger \eta +\frac{1}{2})=\hbar \omega\,(N+\frac{1}{2})$$

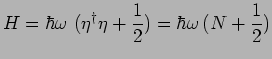On vérifie aisément la relation de commutation :

$$[\eta, \eta^\dagger]=1$$

d'où résultent les relations :

$$N\,\eta = \eta\,(N-1)$$

$$N\,\eta^\dagger = \eta^\dagger \,(N+1)$$

Chercher les valeurs de $H$ revient à chercher celles de $N$ .