Cette généralisation peut s'exercer dans deux directions :
![]() La probabilité cherchée peut concerner plusieurs résultats
possibles de mesure d'une même observable. Ces résultats étant exclusifs
l'un de l'autre, les probabilités partielles s'ajoutent :
La probabilité cherchée peut concerner plusieurs résultats
possibles de mesure d'une même observable. Ces résultats étant exclusifs
l'un de l'autre, les probabilités partielles s'ajoutent :
où encore, en introduisant la projection
![]() du ket
du ket ![]() dans le sous-espace associé aux valeurs
propres
dans le sous-espace associé aux valeurs
propres ![]() et
et ![]() :
:
![]() L'observable mesurée admet un spectre
quelconque (donc mixte) de valeurs propres :
L'observable mesurée admet un spectre
quelconque (donc mixte) de valeurs propres :
chacune d'entre elles pouvant être dégénérée. Cette
dégérescence est levée si on adjoint à ![]() les autres observables,
notées ici globalement
les autres observables,
notées ici globalement ![]() , nécessaires pour former un E.C.O.C.
, nécessaires pour former un E.C.O.C.
La décomposition spectrale de l'état ![]() , sur lequel la mesure de
, sur lequel la mesure de
![]() est effectuée, s'écrit alors :
est effectuée, s'écrit alors :
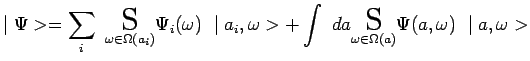 |
![]() (resp.
(resp. ![]() ) désignant l'ensemble des valeurs propres
) désignant l'ensemble des valeurs propres ![]() de
de
![]() associées à la valeur propre dégénérée
associées à la valeur propre dégénérée ![]() (resp.
(resp. ![]() ),
et le symbole S désignant comme précédemment une somme
),
et le symbole S désignant comme précédemment une somme ![]() ou une
intégrale, selon que la variable
ou une
intégrale, selon que la variable ![]() sur laquelle on somme est discrète
ou continue :
sur laquelle on somme est discrète
ou continue :
 |
Ici, comme précédemment, la probabilité concernant la valeur propre ![]() ou un ensemble de valeurs propres
ou un ensemble de valeurs propres
![]() est égale
à la norme de la projection du ket
est égale
à la norme de la projection du ket ![]() dans le sous-espace associé aux
valeurs propres concernées, ou encore égale à la somme des carrés des
modules des composantes de ce vecteur projection.
dans le sous-espace associé aux
valeurs propres concernées, ou encore égale à la somme des carrés des
modules des composantes de ce vecteur projection.
La formulation générale du principe de Born s'exprime comme suit :
|
ou encore, en introduisant les projecteurs :
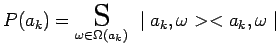 |
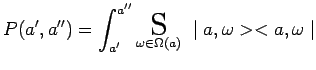 |
et les projections du vecteur ket ![]() représentatif de l'état
initial sur lequel la mesure est effectuée :
représentatif de l'état
initial sur lequel la mesure est effectuée :
Ce postulat peut alors s'énoncer comme suit :
|