c) Conséquences

$\imath-$ Si la mesure de $\hat{A}$ est effectuée sur le système quand il se trouve dans un état propre de $A$ , par exemple $\mid \Psi>=\mid a_j>$ , le résultat de la mesure sera nécessairement :

$$\hat{A}=a_j$$

En effet :

$$\mathcal{P}r(\hat{A}=a_k)=<a_k\mid a_j>=\delta_{kj}$$

Toutefois, et comme nous le verrons dans la suite, si dans un état quantique $\Psi$ exceptionnel, tel que ceux qui viennent d'être envisagé, la valeur $a$ d'une grandeur physique $A$ est affectée d'une probabilité égale à 1, cela ne signifie pas qu'un tel état est équivalent à un état classique dans lequel cette grandeur $A$ vaut $a$ . Cela signifie seulement que si $A$ est mesurée, la valeur $a$ de $A$ sera obtenue. $A$ deviendra égal à $a$ .

Plus généralement, si l'état du système est représenté par un vecteur propre commun à plusieurs observables $A,B,\ldots$ etc :

$$A\,\mid a_i,b_j,\ldots>=a_i\,\mid a_i,b_j,\ldots>\atop B\,\mid a_i,b_j,\ldots>=b_j\,\mid a_i,b_j,\ldots>$$

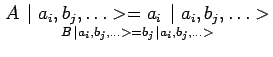il résulte de ce qui précède que la mesure de $\hat{A}$ fournira nécessairement le résultat $a_i$ et celle de $\hat{B}$ le résultat $b_j$ . Nous verrons même que ces deux observables $A$ et $B$ peuvent être mesurées en même temps et qu'à la suite d'une telle mesure on obtiendra le résultat :

$$\hat{A}=a_i~~~~~\mathrm{et}~~~~~\hat{B}=b_j~~~~~\ldots~~~\mathrm{etc}$$

Notamment, à chacun des vecteurs propres $\mid a_i,b_j,c_k,\ldots>$ d'un E.C.O.C. constitué des observables $A,B,C,\ldots$ etc correspond un état physique doté de propriétés physiques bien déterminées, puisque dans cet état, et si les mesures sont faites :

$$\hat{A}=a_i~~~~~~~\hat{B}=b_j~~~~~~~\hat{C}=c_k~~~~~\ldots~~~\mathrm{etc}$$

Ainsi choisir un E.C.O.C., c'est choisir une base représentative constituée d'états physiques bien déterminés, et par rapport auxquels tout autre état physique pourra être reperé. Ces états de base constituent donc ``les pieux'' sur lesquels le formalisme va prendre appui pour rendre compte des observations physiques.

$\imath\imath-$ Inversement, si $N$ mesures effectuées sur $N$ systèmes identiques, tous placés dans le même état $\Psi$ inconnu, fournissent toujours le même résultat :

$$\hat{A}=a_j~~\Longrightarrow~~\mathcal{P}rob~(\,\mid \Psi>=\mid a_j>)~ \underset{N\rightarrow\infty}{\longrightarrow}~1$$

Question 2-2 : Démontrez l'implication précédente.

Les deux conséquences précédentes peuvent être résumées symboliquement comme suit :

$$\mid \Psi>=\mid a_j>~~~~\Longleftrightarrow~~~\hat{A}=a_j$$

$\imath\imath\imath-$ La valeur moyenne de l'observable $A$ dans l'état $\mid \Psi>$ a pour expression :

$$\left<A\right>_\Psi~=~\sum\limits_{k=1}^\infty~a_k~\mathcal{P}_k= \sum\limits_{k=1}^\infty~a_k~\mid <a_k\mid \Psi>\mid ^2$$

$$\left<A\right>_\Psi~=~\sum\limits_{k=1}^\infty~<\Psi\mid a_k>a_k<a_k\mid \Psi>$$

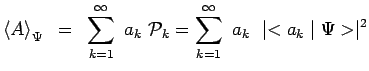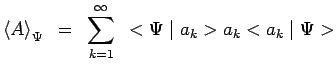et compte tenu d'un résultat antérieur :

$$A=\sum\limits_{k=1}^\infty~\mid a_k>a_k<a_k\mid$$

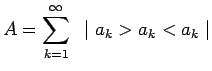d'où :

	$\left<A\right>_\Psi~=~<\Psi\mid A\mid \Psi>~~~~\mathrm{avec}~<\Psi\mid \Psi>=1$

$\imath v-$ La dispersion des valeurs prises, dans l'état $\Psi$ , par l'observable $A$ et autour de sa valeur moyenne $\left<A\right>_\Psi$ est caractérisée par son écart-type $\Delta A_\Psi$ défini par :

$$\Delta A^2_\Psi=<(A-\left<A\right>_\Psi)^2>=\left<A^2\right>_\Psi-\left<A\right>_\Psi^2$$

$v-$ Si $P(a_k)$ désigne le projecteur sur le ket $\mid a_k>$ supposé normalisé :

$$P(a_k)=\mid a_k><a_k\mid ~~~~~\mathrm{avec}~~~<a_k\mid a_k>=1$$

on peut donner encore de la probabilité $\mathcal{P}_k$ deux autres expressions :

	$\mathcal{P}_k~=~<\Psi\mid P(a_k)\mid \Psi>~~~~\mathrm{avec}~<\Psi\mid \Psi>=1$

soit donc la valeur moyenne du projecteur dans l'état $\Psi$ , ou encore en introduisant la projection du ket $\mid \Psi>$ dans le sous-espace $\mathcal{H}_{(a_k)}\subset\,$ $\cal{H}_{\cal{S}}$ associé à la valeur propre $a_k$ :

$$\mid \Psi>=P(a_k)\,\mid \Psi>=\mid a_k><a_k\mid \Psi>$$

	$\mathcal{P}_k~=~<\Psi_k\mid \Psi_k>$

Ces deux expressions de la probabilité $\mathcal{P}_k$ seront généralisées ci-après.