Considérons le système le plus simple, celui constitué d'une seule particule de
spin nul. On peut montrer que les trois observables de position ![]() (définies par référence à un repère
(définies par référence à un repère ![]() ) constituent un E.C.O.C.
Puisque toute valeur réelle positive ou négative est un résultat de mesure
possible, on en déduit que chacune de ces trois observables admet un spectre
continu s'étendant de
) constituent un E.C.O.C.
Puisque toute valeur réelle positive ou négative est un résultat de mesure
possible, on en déduit que chacune de ces trois observables admet un spectre
continu s'étendant de ![]() à
à ![]() . La base constituée des
vecteurs propres communs :
. La base constituée des
vecteurs propres communs :
est la base d'une représentation, dite de Schrödinger. Ces vecteurs de
base peuvent être normalisés à la manière de Dirac, de telle sorte que :
A cette convention d'orthonormalisation correspond la relation de fermeture :
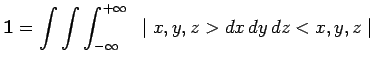 |
de telle sorte que tout ket ![]() représentatif de
l'état
représentatif de
l'état ![]() de la particule peut être décomposé comme suit
:
de la particule peut être décomposé comme suit
:
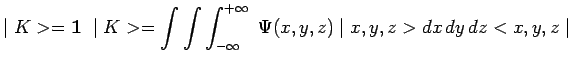 |
avec :
L'état ![]() de la particule est donc parfaitement
caractérisé, sur la base
de la particule est donc parfaitement
caractérisé, sur la base
![]() par la valeur de
ses composantes
par la valeur de
ses composantes
![]() dont l'ensemble constitue ce qui est
appelé la fonction d'onde de la particule.
dont l'ensemble constitue ce qui est
appelé la fonction d'onde de la particule.
La décomposition spectrale précédente permet d'appliquer
immédiatement le postulat III à la mesure d'une ou plusieurs
des trois observables ![]() et en particulier, si
et en particulier, si
![]() :
:
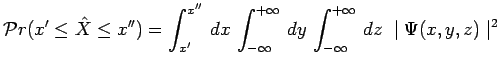 |
|
Si l'élément de volume ![]() est infinitésimal et entoure un point
est infinitésimal et entoure un point
![]() de coordonnées
de coordonnées
![]() , cette probabilité est
proportionnelle à
, cette probabilité est
proportionnelle à ![]() et s'écrit :
et s'écrit :
Ainsi le carré du module de la fonction d'onde de Schrödinger est une densité de
probabilité :
et la fonction d'onde
![]() elle-même est une amplitude de
densité de probabilité.
elle-même est une amplitude de
densité de probabilité.
Supposer l'existence permanente de la particule, implique qu'à chaque instant
la probabilité de la localiser n'importe où dans l'espace est égale à 1,
de telle sorte que nécessairement :
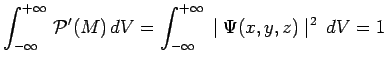 |
Ainsi, nécessairement toute fonction d'onde n'est susceptible de
représenter un état physique de la particule que si la condition
précédente peut être satisfaite. On remarque que cette
condition est seulement l'expression de la normalisation possible
du vecteur ket ![]() image de l'état physique :
image de l'état physique :
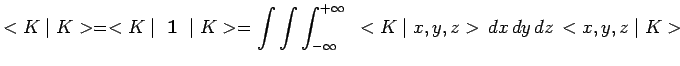 |
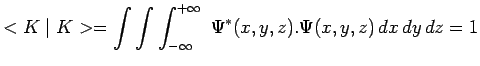 |
Ainsi la représentation de Schrödinger constitue une représentation du formalisme
de Dirac dans laquelle chaque vecteur ket ![]() est représenté par une
fonction d'onde image, de carré sommable.
est représenté par une
fonction d'onde image, de carré sommable.
L'espace de Hilbert
![]() des états devient alors un espace fonctionnel noté
des états devient alors un espace fonctionnel noté
![]() constitué des fonctions de variables réelles
constitué des fonctions de variables réelles ![]() de
carré sommable. Cet espace fonctionnel est une réalisation de
de
carré sommable. Cet espace fonctionnel est une réalisation de
![]() en ce
sens que chaque élément abstrait du formalisme construit dans
en ce
sens que chaque élément abstrait du formalisme construit dans
![]() y sera
représenté par un objet mathématique avec lequel des calculs peuvent
être effectués. Nous construirons plus tard la représentation
mathématique dans
y sera
représenté par un objet mathématique avec lequel des calculs peuvent
être effectués. Nous construirons plus tard la représentation
mathématique dans
![]() des opérateurs et notamment des
observables définies dans
des opérateurs et notamment des
observables définies dans
![]() .
.
On montrera plus tard que les trois composantes de l'impulsion d'une
particule de spin nul,
![]() , constituent un autre E.C.O.C. auquel
correspond une autre base formée des vecteurs propres communs aux trois
observables
, constituent un autre E.C.O.C. auquel
correspond une autre base formée des vecteurs propres communs aux trois
observables
![]() , dont chacune admet un spectre continu s'étendant de
, dont chacune admet un spectre continu s'étendant de
![]() à
à ![]() :
:
et :
de telle sorte que, pour tout état ![]() :
:
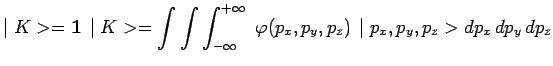 |
avec
![]() .
.
et, comme précédemment, il résulte du postulat III :
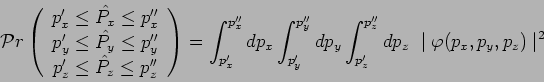 |
et :
Ici encore, puisque toute mesure de l'impulsion de la particule fournit
nécessairement un résultat :
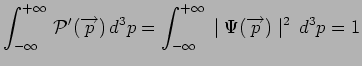 |
et, ici encore, cette condition exprime la normalisation du vecteur ket :
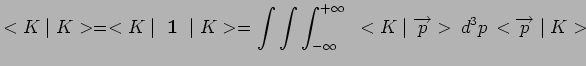 |
 |
Sur la base
![]() constituée des états
propres des observables impulsion
constituée des états
propres des observables impulsion
![]() , le même
vecteur
, le même
vecteur ![]() est donc représenté mathématiquement par
une autre fonction
est donc représenté mathématiquement par
une autre fonction
![]() de carré
sommable, et l'ensemble de ces fonctions constitue une autre
réalisation fonctionnelle, notée
de carré
sommable, et l'ensemble de ces fonctions constitue une autre
réalisation fonctionnelle, notée
![]() de
l'espace de Hilbert
de
l'espace de Hilbert
![]() des états.
des états.
Ainsi, le même vecteur ket ![]() (et donc l'état physique qui
lui correspond) peut être caractérisé et défini, soit par
une fonction
(et donc l'état physique qui
lui correspond) peut être caractérisé et défini, soit par
une fonction
![]() dans l'espace
dans l'espace
![]() rapporté aux
états propres de position, soit par une autre fonction
rapporté aux
états propres de position, soit par une autre fonction
![]() si le même espace
si le même espace
![]() est rapporté
aux états propres d'impulsion. Ces deux représentations sont
reliées par une transformation, résultant de ce changement de
base, et qu'il est facile de préciser.
est rapporté
aux états propres d'impulsion. Ces deux représentations sont
reliées par une transformation, résultant de ce changement de
base, et qu'il est facile de préciser.
Pour simplifier, mais seulement l'écriture, considérons le cas d'un espace
physique fictif, à une seule dimension. L'observable ![]() constitue alors à
elle-seule un E.C.O.C. et on remarque :
constitue alors à
elle-seule un E.C.O.C. et on remarque :
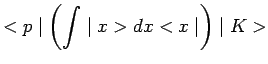 |
|||
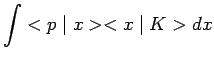 |
soit, en introduisant les fonctions d'onde :
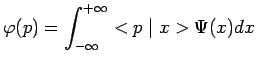 |
généralisation au cas continu de la transformation matricielle
bien connu dans un changement de base :
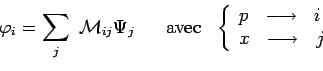 |
Les éléments de la matrice généralisée ![]() seront déterminés plus tardII4 et
trouvés égaux à :
seront déterminés plus tardII4 et
trouvés égaux à :
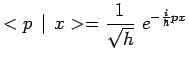 |
de telle sorte que
![]() et
et ![]() sont reliées par des
transformations de Fourier :
sont reliées par des
transformations de Fourier :
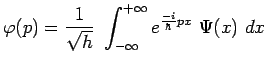 |
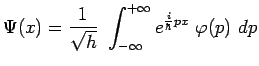 |
Question 2-4 : Déduire des deux expressions précédentes que :
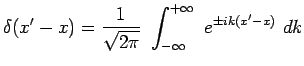 |
Question 2-5 : Ecrire explicitement et complètement l'expression
mathématique qui relie les deux fonctions :
représentatives du même vecteur ket ![]() sur
les deux bases :
sur
les deux bases :