b) La réduction du paquet d'ondes réalise un filtrage

Toute mesure effectuée sur des systèmes microscopiques : des particules en général, concerne un très garnd nombre de systèmes identiques. c'est le cas, par exemple, de la mesure effectuée avec un aimant de Stern et Gerlach^II8 de la composante du spin des

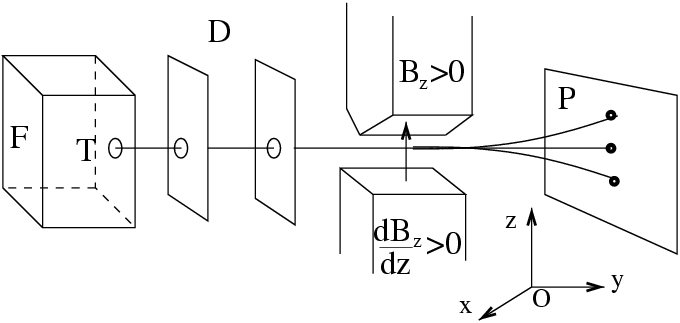
atomes, de spin , d'un jet émis par un four . Après traversée de l'aimant et détection, ces atomes se trouvent distribués en trois sous-ensembles, ceux pour lesquels , ceux pour lesquels et ceux pour lesquels .

La mesure réalise donc une partition de l'ensemble. On peut ensuite poursuivre des mesures ultérieures seulement sur les atomes de l'un de ces trois sous-ensembles, qui ont été ainsi sélectionnés ou filtrés^II8.

D'une façon analogue, ceux des photons qui traversent une lame cristalline de tourmaline en sortent polarisés dans la direction perpendiculaire à celle de l'axe optique du cristal. Ces photons ont ainsi été filtrés et préparés dans un tel état de polarisation^II9.

Il y a lieu de remarquer que les préparations ou les filtrages qui viennent d'être examinés ne deviennent complets, que si la mesure considérée concerne un ensemble complet d'observables qui commutent.

En effet, nous allons préciser comment procéder pour placer un ou plusieurs systèmes identiques dans un état parfaitement déterminé par un ensemble de propriétés physiques choisies mais compatibles.

Chacune de ces propriétés est définie par la valeur propre d'une observable, et nous avons montré, qu'un ensemble maximal de telles propriétés simultanées :

est défini par l'ensemble des valeurs propres de l'E.C.O.C. constitué des observables images des propriétés choisies.

Supposons que nous disposions d'un très grand nombre de systèmes identiques. Quel que soit l'état initial de chacun de ces systèmes :

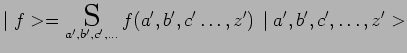la mesure de avec pour résultat , placera (par réduction du paquet d'ondes) un sous-ensemble de ces systèmes dans des états de la forme :

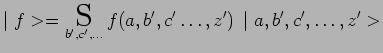De même, une mesure, immédiatement consécutive de avec pour résultat , placera un sous-ensemble de ces systèmes dans des états de la forme :

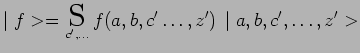et ainsi de suite, avec :

de telle sorte qu'au terme de ces filtrages successifs, tous les système s concernés seront tous dans un même état physique représenté par le ket suivant :

et dans cet état tous ces systèmes jouissent des mêmes propriétés, à savoir que si ces observables sont mesurées à nouveau, on trouvear bien avec certitude :

L'état final ainsi réalisé n'a été obtenu qu'au prix d'un filtrage, avec élimination de tous les systèmes pour lesquels :

A partir d'un état initial quelconque, il n'est pas possible de mettre un système dans un état choisi a priori. En général, si on sait qu'un système microscopique se trouve dans un certain état bien déterminé, et choisi a priori, ce n'est pas parce que l'on a su l'y mettre, mais parce qu'on l'y a trouvé.

On notera que l'état final réalisé précédemment est indépendant de l'ordre dans lequel les mesures ont été effectuées. Celles-ci peuvent même être parfois réalisées simultanément. C'est pourquoi les grandeurs physiques correspondantes sont dites compatibles.

La détermination de cet état final est maximale en ce sens que cet état ne peut être doté d'une propriété physique supplémentaire indépendante des précédentes. en effet, il a déjà été démontré que toute observable qui commute avec toutes les observables d'un E.C.O.C. est fonction de ces observables. L'état résultant de la mesure d'un E.C.O.C. est donc représenté par un vecteur ket normé défini à un facteur de phase près, où est réel.

Question 2-6 : Montrez comment l'expérience révèle la compatibilité des observables de position d'une particule. Indiquez d'autres expériences qui révèlent la compatibilité d'autres observables.