Toute mesure implique nécessairement une interaction entre le système physique étudié (le plus souvent microscopique) et un appareillage macroscopique extérieur à ce système et dont le fonctionnement est supposé régi valablement par les lois de la physique classiqueII12. Toutefois, un tel couplage entre le système et l'appareil d'observation ne constitue pas une mesure. Pour qu'il le soit, il faut d'abord qu'il trouble aussi peu que possible au sens classique l'état de l'objet observé et surtout ensuite que le résultat de cette mesure soit connu.
D'une part, l'interaction n'est effective que si elle laisse des traces physiques irréversibles du processus effectué. D'autre part, la mesure n'est accomplie que lorsque ces traces ont été repérées par un observateur qui en déduit le résultat de cette mesure.
Si donc le système étudié est initialement dans un état ![]() sur lequel on
mesure l'observable
sur lequel on
mesure l'observable ![]() :
:
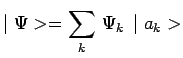 |
au terme de la première étape, le système se trouve placé, d'une
façon irréversible, dans l'un des états ``![]() '' et avec une
probabilité
'' et avec une
probabilité
![]() :
:
Cette interaction a donc eu pour effet d'un point de vue informationnel de
remplacer l'état pur ``![]() '' par un mélange statistique
'' par un mélange statistique
![]() :
:
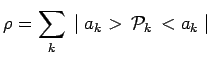 |
On notera que cette première étape est un processus irréversible, spécifiquement quantique. On notera également que sa description est boiteuse puisque l'objet étudié est traité quantiquement tandis que l'appareillage macroscopique est traité classiquement.
La deuxième étape consiste à relever parmi tous ces résultats possibles, lequel a été effectivement obtenu, soit par exemple, dans le cas d'une mesure de position : où est apparue la tache sur la plaque photographique.
L'ensemble de ces deux étapes est résumé par le mécanisme de réduction du paquet d'ondes.
Il est clair que l'opérateur densité ![]() donne de l'état d'un système une
connaissance plus réduite que le vecteur ket
donne de l'état d'un système une
connaissance plus réduite que le vecteur ket ![]() . En effet, connaître
. En effet, connaître
![]() c'est connaître seulement les quantités
c'est connaître seulement les quantités
![]() c'est-à-dire
seulement les modules des coefficients
c'est-à-dire
seulement les modules des coefficients ![]() :
:
où les phases ![]() demeurent indéterminées.
demeurent indéterminées.
Les valeurs moyennes calculées précédemment peuvent encore s'exprimer en
fonction des phases :
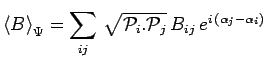 |
Si nous moyennons à nouveau sur les phases inconnues
![]() tous les éléments
tous les éléments ![]() s'annulent et on
retrouve le résultat relatif à un cas pur :
s'annulent et on
retrouve le résultat relatif à un cas pur :
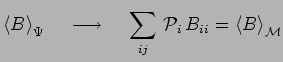 |
Nous verrons plus tard comment certaines théories de la mesure supposent
qu'à la suite d'une simple interactionII13 avec un appareillage de mesure (celle de ![]() par exemple) le vecteur
ket
par exemple) le vecteur
ket ![]() initial deviendrait :
initial deviendrait :
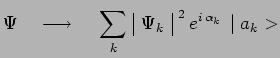 |
les phases ![]() dépendant de chaque mesure individuelle, et
d'une façon totalement aléatoire. Cette interprétation qui vise à
évacuer les paradoxes de la mesure prête largement à contestations.
dépendant de chaque mesure individuelle, et
d'une façon totalement aléatoire. Cette interprétation qui vise à
évacuer les paradoxes de la mesure prête largement à contestations.
En résumé, il y a lieu de distinguer nettement :
![]() Le cas pur, décrit par un vecteur ket défini
à un facteur de phase près, et auquel sont associées des
probabilités seulement potentielles, c'est-à-dire qui ne seront
réalisées que si une mesure est faite. Le ket
Le cas pur, décrit par un vecteur ket défini
à un facteur de phase près, et auquel sont associées des
probabilités seulement potentielles, c'est-à-dire qui ne seront
réalisées que si une mesure est faite. Le ket ![]() annonce, avec la probabilité
annonce, avec la probabilité
![]() que si
que si
![]() est mesuré, l'état du système après mesure,
devra être représenté par le ket
est mesuré, l'état du système après mesure,
devra être représenté par le ket ![]() .
.
![]() Le mélange, représenté par
l'opérateur
Le mélange, représenté par
l'opérateur ![]() . Si le système étudié est unique
l'opérateur densité
. Si le système étudié est unique
l'opérateur densité ![]() dit que ce système, avant
toute mesure éventuelle, se trouve déjà dans un des
états
dit que ce système, avant
toute mesure éventuelle, se trouve déjà dans un des
états ![]() avec la probabilité
avec la probabilité
![]() . Cette
probabilité n'est nullement prévisionnelle ou conditionnée
par une mesure. C'est une probabilité déjà réalisée et
donc du type classique.
. Cette
probabilité n'est nullement prévisionnelle ou conditionnée
par une mesure. C'est une probabilité déjà réalisée et
donc du type classique.
Si ![]() décrit un ensemble de
décrit un ensemble de ![]() systèmes identiques, l'opérateur
systèmes identiques, l'opérateur ![]() dit
que ces
dit
que ces ![]() systèmes ne sont pas tous dans le même état initial, mais que :
systèmes ne sont pas tous dans le même état initial, mais que :
systèmes se trouvent déjà dans l'état ![]() .
.
Il faut enfin remarquer que les états ![]() considérés
ci-dessus sont en même temps les vecteurs propres de
considérés
ci-dessus sont en même temps les vecteurs propres de ![]() , et
ceux qui diagonalisent l'opérateur
, et
ceux qui diagonalisent l'opérateur ![]() . Une telle
coïncidence n'est pas nécessaire.
. Une telle
coïncidence n'est pas nécessaire.
D'une façon plus générale l'opérateur densité peut être défini
par sa fonction, c'est-à-dire tel que, quelle que soit l'observable ![]() :
:
Comme nous le verrons, cette définition permet de déterminer la
représentation matricielle ![]() de
de ![]() sur une base quelconque :
sur une base quelconque :
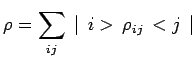 |
La matrice ![]() , hermitique comme nous l'avons déjà remarqué, peut être
diagonalisée sur la base constituée de ses vecteurs propres orthonormés et
prend la forme standard précédente :
, hermitique comme nous l'avons déjà remarqué, peut être
diagonalisée sur la base constituée de ses vecteurs propres orthonormés et
prend la forme standard précédente :
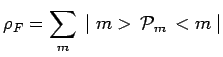 |