Il est donc nécessaire de bien distinguer un état, codé par un vecteur ket, et un mélange d'états. Cette distinction doit être prise en compte par le formalisme en introduisant un nouvel être mathématique pour coder un tel mélange.
Il est peut-être utile de rappeler une dernière fois que ce
mélange peut être constitué de ![]() micro-systèmes identiques
dont
micro-systèmes identiques
dont
![]() ) se trouvent dans l'état codé
) se trouvent dans l'état codé
![]() ou peut être constitué d'un seul micro-système dont
on sait qu'il se trouve effectivementII11, avec la probabilité
ou peut être constitué d'un seul micro-système dont
on sait qu'il se trouve effectivementII11, avec la probabilité
![]() , dans l'un
de ces états codés
, dans l'un
de ces états codés ![]() .
.
Dans l'un ou l'autre cas la situation physique sera représentée
dans le formalisme par un opérateur qui caractérise la
densité
![]() des états codés
des états codés ![]() dans le
mélange. Pour cette raison, cet opérateur caractéristique
est appelé l'opérateur densité du mélange et
s'écrit comme une somme des projecteurs :
dans le
mélange. Pour cette raison, cet opérateur caractéristique
est appelé l'opérateur densité du mélange et
s'écrit comme une somme des projecteurs :
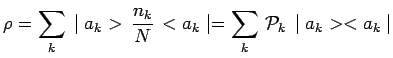 |
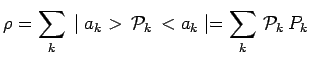 |
Sur toute base de représentation, constituée des vecteurs
![]() orthonormés, l'opérateur densité
orthonormés, l'opérateur densité ![]() sera
lui-même représenté par une matrice appelée matrice
densité :
sera
lui-même représenté par une matrice appelée matrice
densité :
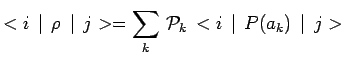 |
En particulier sur la base
![]() la matrice est
diagonale :
la matrice est
diagonale :
Notamment, si le mélange se réduit à un seul terme :
ce mélange décrit le même état que le vecteur
ket ![]() . On dit que ce mélange se réduit à un cas
pur
. On dit que ce mélange se réduit à un cas
pur ![]() . Plus généralement, tout état
. Plus généralement, tout état ![]() codé
par le vecteur ket normé
codé
par le vecteur ket normé ![]() peut également être codé par
l'opérateur densité :
peut également être codé par
l'opérateur densité :
Avec cette nouvelle notation, les résultats précédents s'écrivent très
simplement, comme suit, dans le cas général :
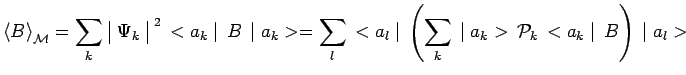 |
et de même par ailleurs avec
![]() :
:
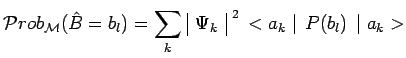 |
Ce dernier résultat peut encore s'écrire :
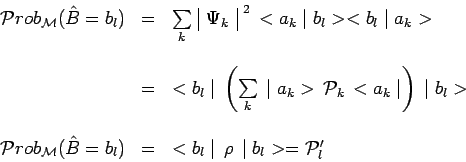 |
Cette probabilité est également celle de trouver, à l'issue
d'une mesure de ![]() , le système dans l'état pur
, le système dans l'état pur ![]() .
Plus généralement, la probabilité de trouver le mélange
``
.
Plus généralement, la probabilité de trouver le mélange
``![]() '' dans un état ``
'' dans un état ``![]() '' a pour expression :
'' a pour expression :
La matrice densité
![]() consécutive à la mesure de
consécutive à la mesure de ![]() a
donc pour expression :
a
donc pour expression :
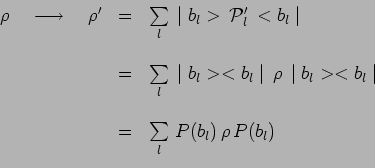 |
et diffère donc de la matrice densité initiale :
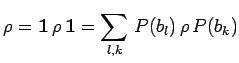 |
Ainsi la mesure de ![]() a pour effet d'annuler tous les éléments non
diagonaux de la représentation matricielle de
a pour effet d'annuler tous les éléments non
diagonaux de la représentation matricielle de ![]() sur les états propres
de
sur les états propres
de ![]() .
.